↓Skip to main content

【LeetCode 684】冗余连接

·244 words·2 mins
WFUing
Author
WFUing
A graduate who loves coding.
Table of Contents

  • 链接：https://leetcode.cn/problems/redundant-connection/description/

难点
#

是第一次刷并查集的题目，比较陌生了。

给出一个并查集的模版：

public static class UnionFind {
  private int[] parent;
  private int[] sizeMap;
  private int size;

  public UnionFind(int N) {
      size = N;
      parent = new int[N];
      sizeMap = new int[N];
      for (int i = 0; i < N; i++) {
          parent[i] = i;
          sizeMap[i] = 1;
      }
  }

  public int size() {
      return size;
  }

  private int find(int v) {
      if (v != parent[v]) {
          parent[v] = find(parent[v]);
      }
      return parent[v];
  }

  public void union(int v1, int v2) {
      int f1 = find(v1);
      int f2 = find(v2);
      if (f1 != f2) {
          size--;
          int s1 = sizeMap[f1];
          int s2 = sizeMap[f2];
          if (s1 > s2) {
              parent[f2] = f1;
              sizeMap[f1] += s2;
          } else {
              parent[f1] = f2;
              sizeMap[f2] += s1;
          }
      }
  }
}

分析
#

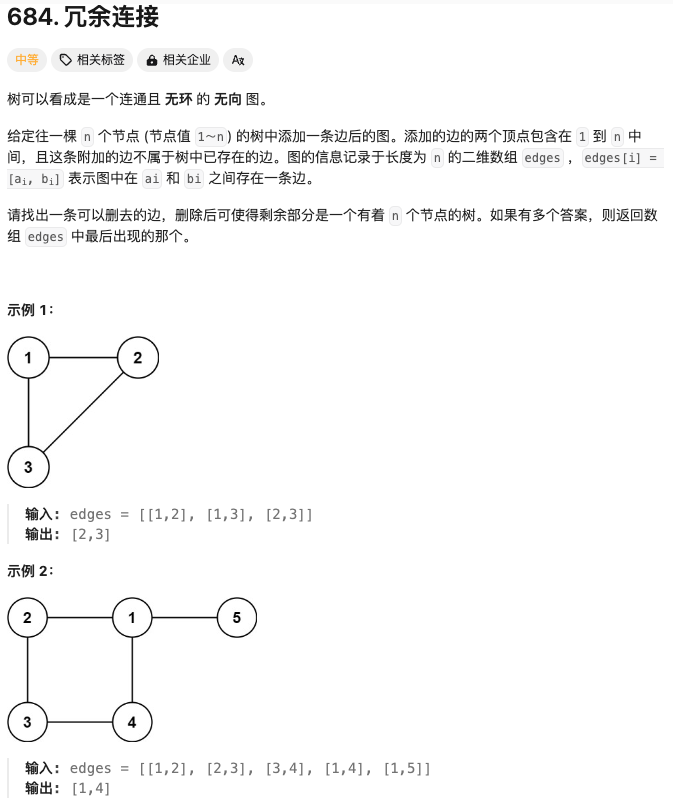
在一棵树中，边的数量比节点的数量少 $1$。如果一棵树有 $n$ 个节点，则这棵树有 $n−1$ 条边。这道题中的图在树的基础上多了一条附加的边，因此边的数量也是 $n$。

树是一个连通且无环的无向图，在树中多了一条附加的边之后就会出现环，因此附加的边即为导致环出现的边。

可以通过并查集寻找附加的边。初始时，每个节点都属于不同的连通分量。遍历每一条边，判断这条边连接的两个顶点是否属于相同的连通分量。

  • 如果两个顶点属于不同的连通分量，则说明在遍历到当前的边之前，这两个顶点之间不连通，因此当前的边不会导致环出现，合并这两个顶点的连通分量。
  • 如果两个顶点属于相同的连通分量，则说明在遍历到当前的边之前，这两个顶点之间已经连通，因此当前的边导致环出现，为附加的边，将当前的边作为答案返回。

代码
# 

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
        int[] par = new int[n + 1];

        for (int i = 1; i <= n; i++) {
            par[i] = i;
        }

        for (int i = 0; i < n; i++) {
            if (find(par, edges[i][0]) != find(par, edges[i][1])) {
                union(par, edges[i][0], edges[i][1]);
            } else {
                return edges[i];
            }
        }

        return new int[0];
    }

    public int find(int[] par, int v) {
        if (v != par[v]) {
            par[v] = find(par, par[v]);
        }

        return par[v];
    }

    public void union(int[] par, int v, int u) {
        par[find(par, v)] = find(par, u);
    }
}

💬评论