↓Skip to main content

【LeetCode 72】编辑距离

·90 words·1 min
WFUing
Author
WFUing
A graduate who loves coding.
Table of Contents

  • 链接：https://leetcode.cn/problems/edit-distance/description/

难点
#

在我二刷这道题的时候，还是卡了一会，主要有三个难点：

  • dp数组表示什么
  • 如何初始化dp数组
  • 如何针对题目告诉我们的三种操作，实现dp数组的更新

当然这也是动态规划数组的三个难点，需要重点培养这种感觉，形成正确的判断直觉。

分析
#

在这题里，$dp[i][j]$ 定义为 $word1_{1:i}$ 转换成 $word2_{1:j}$ 所需要的最小步数。

按照对 $dp[i][j]$ 的定义，很快就可以得到下面的初始化值：

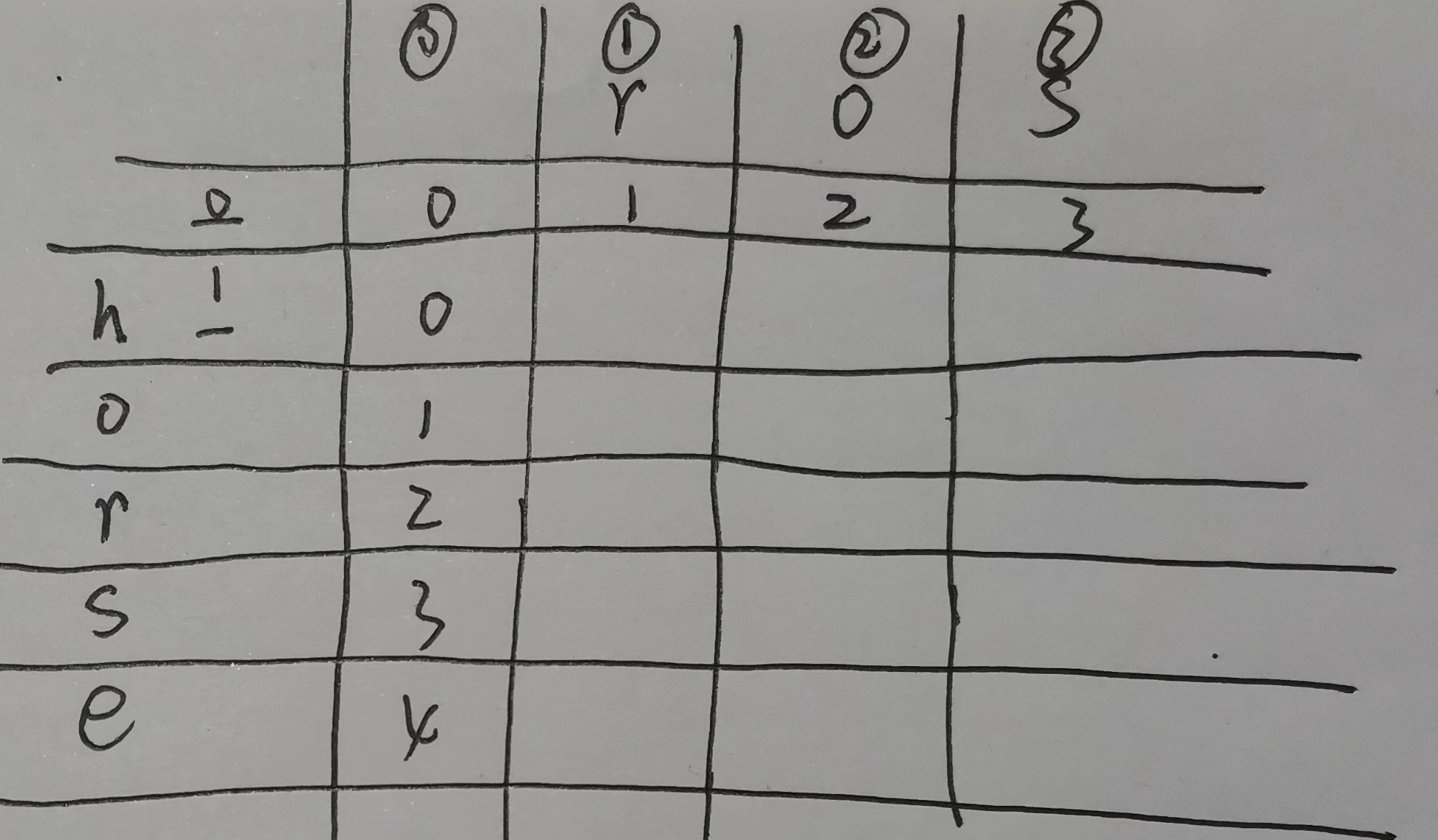
三种操作，结合 $dp[i][j]$ 就可以得出下面两种情况：

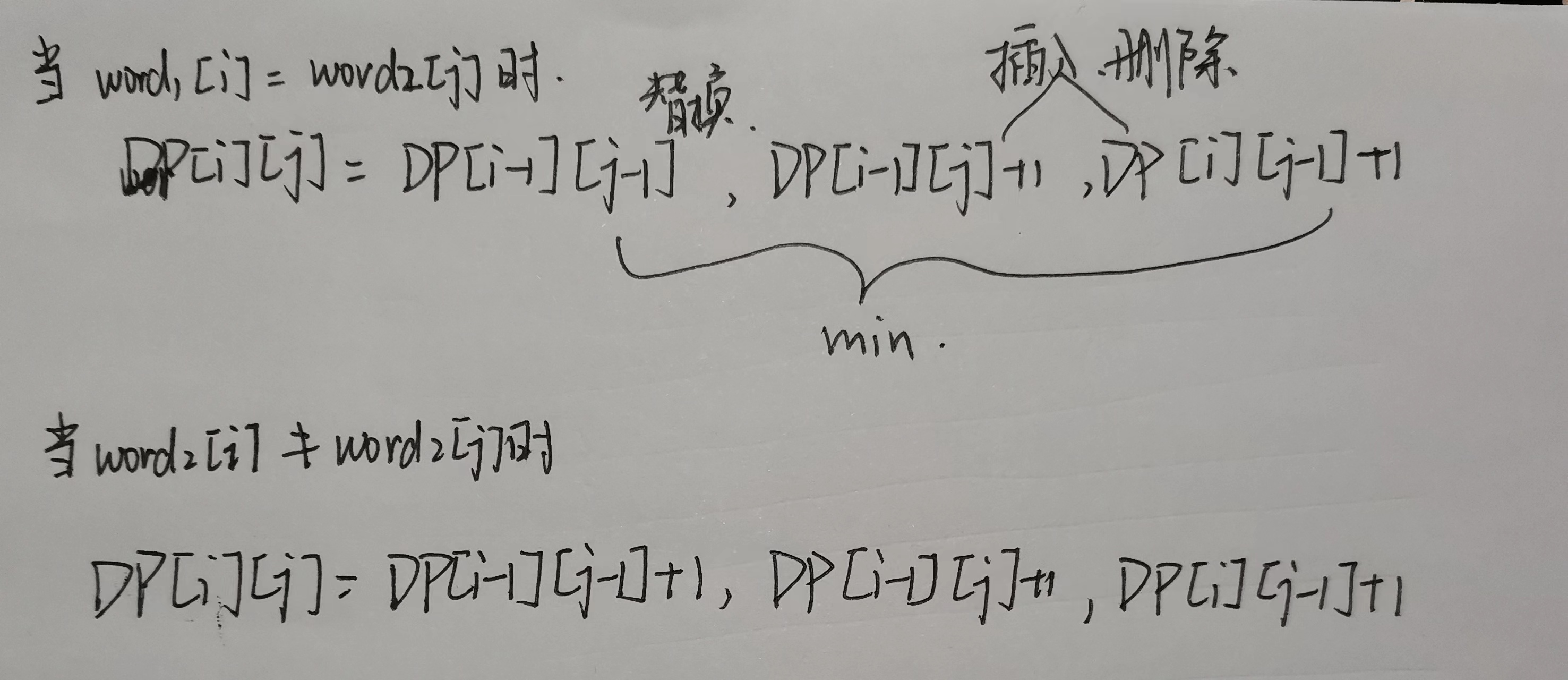
代码
# 

class Solution {
    public int minDistance(String word1, String word2) {
        int len1 = word1.length(), len2 = word2.length();
        int[][] dp = new int[len1+1][len2+1];
        for(int i=0;i<=len1;i++) {
            dp[i][0] = i;
        }
        for(int i=0;i<=len2;i++) {
            dp[0][i] = i;
        }
        for(int i=1;i<=len1;i++) {
            for(int j=1;j<=len2;j++) {
                if(word1.charAt(i-1) == word2.charAt(j-1)) {
                    dp[i][j] = Math.min(dp[i-1][j-1], Math.min(dp[i-1][j]+1, dp[i][j-1]+1));
                } else {
                    dp[i][j] = Math.min(dp[i-1][j-1]+1, Math.min(dp[i-1][j]+1, dp[i][j-1]+1));
                }
            }
        }
        return dp[len1][len2];
    }
}