↓Skip to main content

【LeetCode 368】最大整除子集

·266 words·2 mins
WFUing
Author
WFUing
A graduate who loves coding.
Table of Contents

  • 链接：https://leetcode.cn/problems/largest-divisible-subset/description/

难点
#

难点在于如何记录答案，最后把最大整除子集输出。幸运的是，题目没有限制输出的字典序，只要输出的是合理答案就可以。

代码
# 

class Solution {
    public List<Integer> largestDivisibleSubset(int[] nums) {
        Arrays.sort(nums);
        int n = nums.length;
        int[] dp = new int[n];
        int[] cnt = new int[n];
        for(int i = n-2; i >=0 ; i--) {
            for(int j = n-1; j > i; j--) {
                if(nums[j] % nums[i] == 0 && dp[j] + 1 > dp[i]) {
                    dp[i] = dp[j] + 1;
                    cnt[i] = j;
                }
            } 
        }
        int maxx = Arrays.stream(dp).max().getAsInt();
        List<Integer> ans = new ArrayList<>();
        for(int i = 0; i < n; i++) {
            if(dp[i] == maxx) {
                ans.add(nums[i]);
                int temp = cnt[i];
                while(temp != 0) {
                    i = cnt[i];
                    temp = cnt[i];
                    ans.add(nums[i]);
                }
                break;
            }
        }
        return ans;
    }
}

当然，用题解中的方法也可以，举个例子

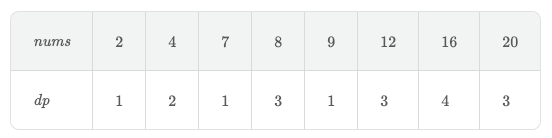
上图中 dp 为 4 的 16，肯定可以整除一个 dp 为 3 的，上面的就是 8，以此类推，得到结果。

class Solution {
    public List<Integer> largestDivisibleSubset(int[] nums) {
        int len = nums.length;
        Arrays.sort(nums);

        // 第 1 步：动态规划找出最大子集的个数、最大子集中的最大整数
        int[] dp = new int[len];
        Arrays.fill(dp, 1);
        int maxSize = 1;
        int maxVal = dp[0];
        for (int i = 1; i < len; i++) {
            for (int j = 0; j < i; j++) {
                // 题目中说「没有重复元素」很重要
                if (nums[i] % nums[j] == 0) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }

            if (dp[i] > maxSize) {
                maxSize = dp[i];
                maxVal = nums[i];
            }
        }

        // 第 2 步：倒推获得最大子集
        List<Integer> res = new ArrayList<Integer>();
        if (maxSize == 1) {
            res.add(nums[0]);
            return res;
        }
        
        for (int i = len - 1; i >= 0 && maxSize > 0; i--) {
            if (dp[i] == maxSize && maxVal % nums[i] == 0) {
                res.add(nums[i]);
                maxVal = nums[i];
                maxSize--;
            }
        }
        return res;
    }
}