总纲 #
课程的教学目标:掌握蛮力、分治、减治、边治和时空权衡等算法设计思想的特点。
- 能够熟练使用蛮力法解决问题,作为优化的基线方法,例如找到数组中大小最接近的两个元素的差、找到凸包极点等问题
- 分治思想在具体实现的时候,可以使用递归的方法,也可以结合特殊的数据结构使用循环的方法,例如合并排序、快速排序等
- 能够采用分治思想解决的两个经典问题是最近对问题和凸包问题,请掌握具体的代码实现
- 时空权衡思想在算法设计中应用非常广泛,例如字符串匹配、B树,乃至动态规划,都和时间权衡有关,需要熟练掌握
- 贪心法的思想和特点,用贪心法解决经典问题,最小生成树、活动相容等。
- 动态规划的思想和特点,针对以下经典问题能写出子问题的递归式,描述算法思想和伪代码:最长公共子序列(最长回文子序列)和矩阵连乘问题
- 了解平滑函数性质,能用主定理求解递归方程,判断当前方程适用主定理哪一类型,进而解出递归式。
- 复杂度的表示式:$O(f)$、$\Omega (f)$、$\Theta (f)$的含义,基于三种表示的一系列性质
- 介绍NPC理论的含义和实际应用价值,能列举NPC问题,证明一些主要的NPC问题(如装箱问题,0-1背包)既是NP的也是NP-hard的
- 近似算法的定义,如何衡量近似算法的好坏,能掌握对于装箱问题的几种贪心算法(First Fit Algorithm - FF,Next Fit Algorithm - NF,First Fit Decreasing - FFD)。在线算法的定义,以上哪个算法是在线算法,复杂度如何。
上面10个点,每个点是一道题,每题10分,包括题型:
- 给模板填空题(比如使用 Prim、Kruskal 构造最小生成树的过程中,给出前几步,让你补完过程
- 讨论题和问答题(比如大O(f)的含义
- 写伪代码的题
调分
- 不管出什么题,你写点相关的定义都有保底分;
- 不会也要写,好调分;
答疑
- 邮箱联系
- 可以约办公室 office hour
上图的‘例如’ 就是对应题型的考试范围;
- 蛮力法:找数组中大小最接近的两个元素、凸包极点… 就从这些里面选考
前半部分是李传艺老师授课、出题,后半部分是李言辉老师授课、出题。李言辉后面着重复习了自己的部分。
- 课本: 算法设计与分析基础.第3版
- 往年卷: 可参考题型
1. 蛮力法 #
蛮力法(Brute Force)是一种通过遍历所有可能的解决方案来解决问题的算法。尽管其时间复杂度通常较高,但它简单直接,适用于规模较小的问题或作为其他优化算法的基线方法。以下是对蛮力法及其在两个具体问题中的应用介绍:
1. 数组中大小最接近的两个元素的差
问题描述: 给定一个包含 $n$ 个整数的数组,找到数组中差值最小的两个元素。
蛮力法:
- 初始化一个最小差值变量
minDiff,并设置为一个足够大的值。 - 使用两层嵌套循环遍历数组中的每一对元素。
- 对于每一对元素,计算它们的差的绝对值。
- 如果计算得到的差小于
minDiff,则更新minDiff。 - 最后,返回
minDiff。
public class MinDiff {
public static int findMinDiff(int[] arr) {
int n = arr.length;
int minDiff = Integer.MAX_VALUE;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int diff = Math.abs(arr[i] - arr[j]);
if (diff < minDiff) {
minDiff = diff;
}
}
}
return minDiff;
}
public static void main(String[] args) {
int[] arr = {3, 8, 15, 17};
System.out.println("The minimum difference is: " + findMinDiff(arr));
}
}
2. 找到凸包极点
问题描述: 给定一个二维平面上的点集,找到这些点的凸包极点(形成凸包的最外层点)。
蛮力法:
- 初始化一个空列表
hullPoints用于存储凸包极点。 - 使用两层嵌套循环,遍历每一对点。
- 对于每一对点,假设这两个点是凸包的一条边,检查其他所有点是否都在这条边的同一侧。
- 如果某条边的假设成立,则将构成这条边的两个点加入
hullPoints - 去除重复点,最终得到凸包极点。
import java.util.ArrayList;
import java.util.List;
public class ConvexHull {
public static class Point {
int x, y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
// 计算向量 (o -> a) 和 (o -> b) 的叉积
public static int crossProduct(Point o, Point a, Point b) {
return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);
}
public static List<Point> convexHull(Point[] points) {
int n = points.length;
if (n < 3) return List.of(points);
List<Point> hullPoints = new ArrayList<>();
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
boolean allLeft = true;
boolean allRight = true;
for (int k = 0; k < n; k++) {
if (k == i || k == j) continue;
int cp = crossProduct(points[i], points[j], points[k]);
if (cp > 0) {
allRight = false;
} else if (cp < 0) {
allLeft = false;
}
if (!(allLeft || allRight)) break;
}
if (allLeft || allRight) {
if (!hullPoints.contains(points[i])) hullPoints.add(points[i]);
if (!hullPoints.contains(points[j])) hullPoints.add(points[j]);
}
}
}
return hullPoints;
}
public static void main(String[] args) {
Point[] points = {
new Point(0, 0),
new Point(1, 1),
new Point(2, 2),
new Point(3, 0),
new Point(0, 3),
new Point(3, 3)
};
List<Point> hull = convexHull(points);
System.out.println("Points in the convex hull:");
for (Point p : hull) {
System.out.println("(" + p.x + ", " + p.y + ")");
}
}
}
叉积的定义和几何意义
给定两个向量 $\mathbf{u}$ 和 $\mathbf{v}$,它们的叉积 $\mathbf{u} \times \mathbf{v}$ 的几何意义为:
- $\mathbf{u} \times \mathbf{v}$ 的符号决定了向量 $\mathbf{v}$ 相对于 $\mathbf{u}$ 的方向:
- 如果结果为正,则 $\mathbf{v}$ 在 $\mathbf{u}$ 的逆时针方向(左侧)。
- 如果结果为负,则 $\mathbf{v}$ 在 $\mathbf{u}$ 的顺时针方向(右侧)。
- 如果结果为零,则 $\mathbf{u}$ 和 $\mathbf{v}$ 共线(点
o、a、b在同一条直线上)。
叉积公式
对于二维平面上的两个向量 $\mathbf{u} = (u_x, u_y)$ 和 $\mathbf{v} = (v_x, v_y)$,它们的叉积公式为:
$$ [ \mathbf{u} \times \mathbf{v} = u_x \cdot v_y - u_y \cdot v_x ] $$
在我们的问题中,向量 $\mathbf{oa}$ 和 $\mathbf{ob}$ 的坐标分别为:
- 向量 $\mathbf{oa}$: $(a.x - o.x, a.y - o.y)$
- 向量 $\mathbf{ob}$: $(b.x - o.x, b.y - o.y)$
因此,向量 $\mathbf{oa}$ 和 $\mathbf{ob}$ 的叉积计算为:
$$ [ (a.x - o.x) \cdot (b.y - o.y) - (a.y - o.y) \cdot (b.x - o.x) ] $$
示例
假设有点 o、a 和 b 的坐标分别为 (0, 0)、(1, 1) 和 (2, 0):
- 向量 $\mathbf{oa}$:(1 - 0, 1 - 0) = (1, 1)
- 向量 $\mathbf{ob}$:(2 - 0, 0 - 0) = (2, 0)
叉积的计算为:
$$ [ (1 \cdot 0) - (1 \cdot 2) = 0 - 2 = -2 ] $$
结果为负,说明点 b 在从点 o 指向点 a 的向量的右侧。
2. 分治 #
分治法(Divide and Conquer)是一种算法设计范式,其核心思想是将一个复杂的问题分解成若干个相似但规模更小的子问题,递归地解决这些子问题,然后将它们的结果合并起来得到原问题的解。分治法广泛应用于许多经典算法中,例如合并排序(Merge Sort)、快速排序(Quick Sort)等。
分治法的步骤
- 分解(Divide): 将问题划分为若干个规模更小的子问题。
- 解决(Conquer): 递归地解决这些子问题。如果子问题规模足够小,可以直接求解。
- 合并(Combine): 将子问题的结果合并成原问题的解。
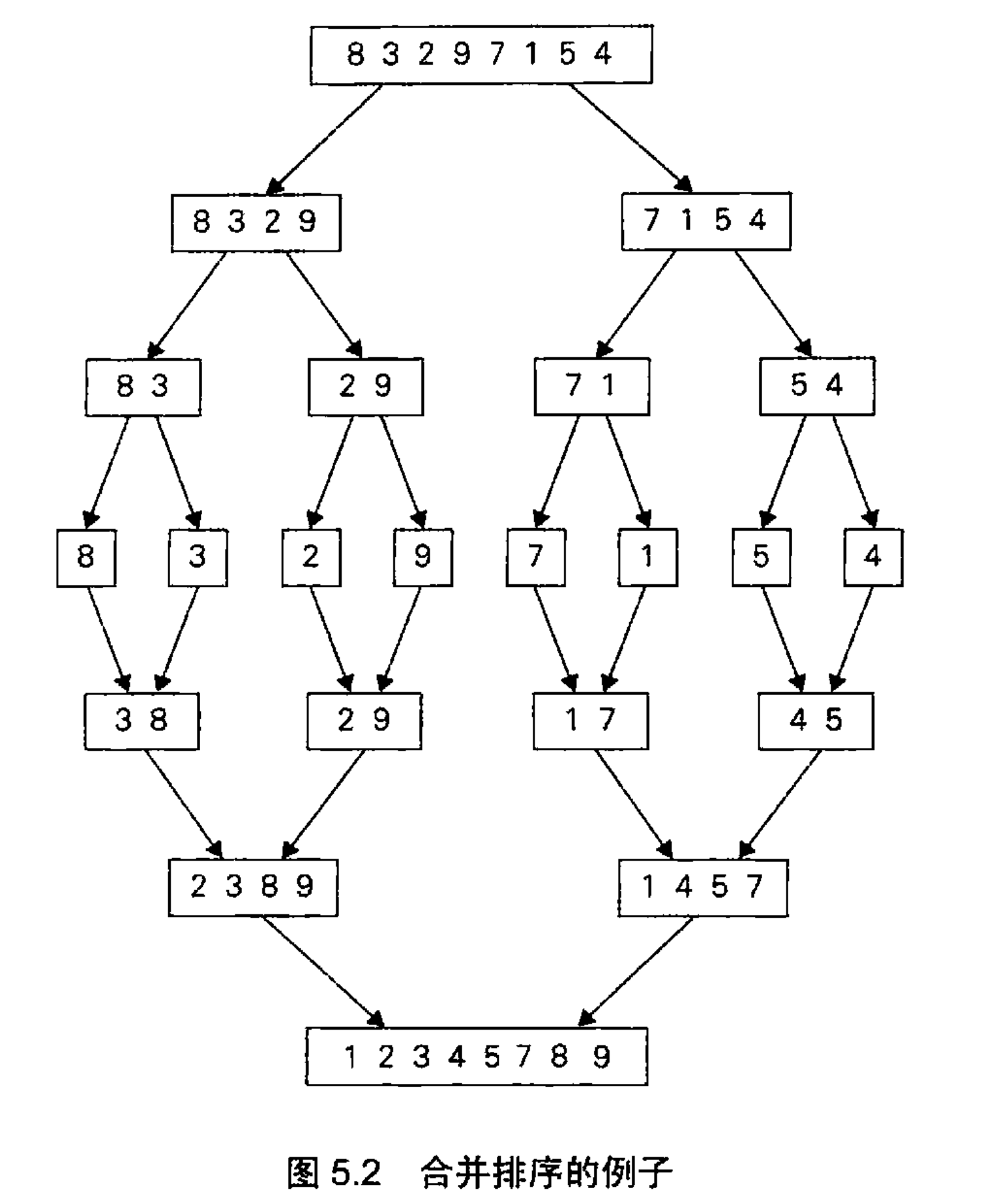
示例 1:合并排序(Merge Sort)
合并排序是一种基于分治法的排序算法。其主要步骤如下:
- 分解: 将待排序数组分成两半。
- 解决: 递归地对每一半进行排序。
- 合并: 将排序好的两半合并成一个有序的数组。


public class MergeSort {
public static void mergeSort(int[] array) {
if (array.length < 2) {
return;
}
int mid = array.length / 2;
int[] left = new int[mid];
int[] right = new int[array.length - mid];
System.arraycopy(array, 0, left, 0, mid);
System.arraycopy(array, mid, right, 0, array.length - mid);
mergeSort(left);
mergeSort(right);
merge(array, left, right);
}
private static void merge(int[] array, int[] left, int[] right) {
int i = 0, j = 0, k = 0;
while (i < left.length && j < right.length) {
if (left[i] <= right[j]) {
array[k++] = left[i++];
} else {
array[k++] = right[j++];
}
}
while (i < left.length) {
array[k++] = left[i++];
}
while (j < right.length) {
array[k++] = right[j++];
}
}
public static void main(String[] args) {
int[] array = {38, 27, 43, 3, 9, 82, 10};
mergeSort(array);
for (int i : array) {
System.out.print(i + " ");
}
}
}
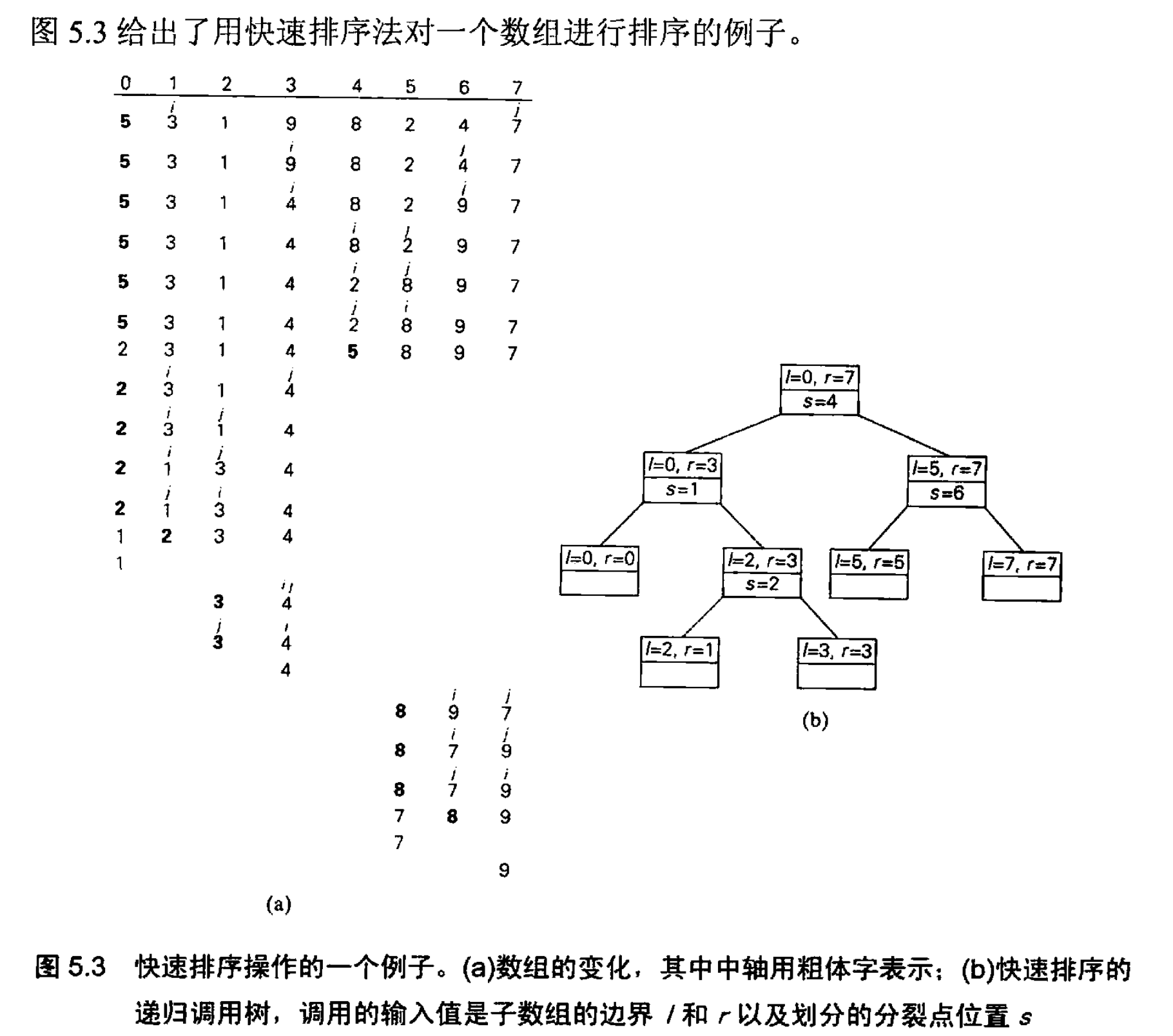
示例 2:快速排序(Quick Sort)
快速排序是一种高效的排序算法,其主要步骤如下:
- 分解: 从数组中选择一个基准元素,将其他元素重新排列,使得比基准元素小的元素放在左边,比基准元素大的元素放在右边。
- 解决: 递归地对基准元素左边的子数组和右边的子数组进行排序。
- 合并: 由于每次分解已经部分排序,所以合并步骤是隐含的。


public class QuickSort {
public static void quickSort(int[] array, int low, int high) {
if (low < high) {
int pi = partition(array, low, high);
quickSort(array, low, pi - 1);
quickSort(array, pi + 1, high);
}
}
private static int partition(int[] array, int low, int high) {
int pivot = array[high];
int i = low - 1;
for (int j = low; j < high; j++) {
if (array[j] < pivot) {
i++;
swap(array, i, j);
}
}
swap(array, i + 1, high);
return i + 1;
}
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
public static void main(String[] args) {
int[] array = {10, 7, 8, 9, 1, 5};
int n = array.length;
quickSort(array, 0, n - 1);
for (int i : array) {
System.out.print(i + " ");
}
}
}
示例 3:最近对问题(Closest Pair Problem)
最近对问题是指在给定的二维平面上找到距离最近的一对点。
基本思想:
- 分解: 将点集按 x 坐标排序,并划分为左右两部分。
- 解决: 递归地找到左右两部分中的最近对。
- 合并: 检查跨越分割线的点对,找到整体的最近对。

import java.util.Arrays;
import java.util.Comparator;
public class ClosestPair {
static class Point {
int x, y;
Point(int x, int y) {
this.x = x;
this.y = y;
}
}
public static double closestPair(Point[] points) {
Point[] px = points.clone();
Arrays.sort(px, Comparator.comparingInt(p -> p.x));
Point[] py = points.clone();
Arrays.sort(py, Comparator.comparingInt(p -> p.y));
return closestPairRec(px, py);
}
private static double closestPairRec(Point[] px, Point[] py) {
int n = px.length;
if (n <= 3) {
return bruteForce(px);
}
int mid = n / 2;
Point midPoint = px[mid];
Point[] pxLeft = Arrays.copyOfRange(px, 0, mid);
Point[] pxRight = Arrays.copyOfRange(px, mid, n);
Point[] pyLeft = Arrays.stream(py).filter(p -> p.x <= midPoint.x).toArray(Point[]::new);
Point[] pyRight = Arrays.stream(py).filter(p -> p.x > midPoint.x).toArray(Point[]::new);
double dLeft = closestPairRec(pxLeft, pyLeft);
double dRight = closestPairRec(pxRight, pyRight);
double d = Math.min(dLeft, dRight);
Point[] strip = Arrays.stream(py).filter(p -> Math.abs(p.x - midPoint.x) < d).toArray(Point[]::new);
return Math.min(d, stripClosest(strip, d));
}
private static double bruteForce(Point[] points) {
double minDist = Double.MAX_VALUE;
for (int i = 0; i < points.length; i++) {
for (int j = i + 1; j < points.length; j++) {
double dist = distance(points[i], points[j]);
if (dist < minDist) {
minDist = dist;
}
}
}
return minDist;
}
private static double stripClosest(Point[] strip, double d) {
double minDist = d;
for (int i = 0; i < strip.length; i++) {
for (int j = i + 1; j < strip.length && (strip[j].y - strip[i].y) < minDist; j++) {
double dist = distance(strip[i], strip[j]);
if (dist < minDist) {
minDist = dist;
}
}
}
return minDist;
}
private static double distance(Point p1, Point p2) {
return Math.sqrt(Math.pow(p1.x - p2.x, 2) + Math.pow(p1.y - p2.y, 2));
}
public static void main(String[] args) {
Point[] points = { new Point(2, 3), new Point(12, 30), new Point(40, 50), new Point(5, 1), new Point(12, 10), new Point(3, 4) };
System.out.println("The smallest distance is " + closestPair(points));
}
}
示例 4:凸包问题(Convex Hull Problem)
#include<bits/stdc++.h>
using namespace std;
#define Double long double
const int MAXN = 1e6 + 10;
struct Point{
Double x,y;
Double rad;
Point(Double x=0,Double y=0):x(x),y(y){}
void read(){
scanf("%Lf %Lf",&x,&y);
//rad = atan2(y,x);
}
};
typedef vector<Point> Polygon;
typedef Point Vector;
inline Vector operator - (Vector A,Vector B){
return Vector(A.x - B.x , A.y - B.y);
}
inline Double Dot(Vector A,Vector B){
return A.x * B.x + A.y * B.y;
}
inline Double Length(Vector A){
return sqrt(Dot(A , A));
}
inline Double Cross(Vector A,Vector B){
return A.x * B.y - A.y * B.x;
}
int N;
Point points[MAXN];
Polygon convex;
bool cmpByX(Point A,Point B){
if(A.x != B.x) return A.x < B.x;
else return A.y < B.y;
}
void findConvex(Point A,Point B,vector<Point> p){
if(!p.size()) return;
Point C = p[0];
vector<Point> l;
vector<Point> r;
for(auto P:p){
if(Cross(B-A,P-A) > Cross(B-A,C-A)) C = P;
}
for(auto P:p){
if(Cross(C-A,P-A) > 0) l.push_back(P);
if(Cross(B-C,P-C) > 0) r.push_back(P);
}
findConvex(A,C,l);
convex.push_back(C);
findConvex(C,B,r);
}
Double getPolygonPerimeter(Polygon polygon){
Double ret = 0;
for(int i = 0;i < polygon.size(); i++){
ret += Length(polygon[(i + 1) % polygon.size()] - polygon[i]);
}
return ret;
}
void solve(){
scanf("%d",&N);
for(int i = 1; i <= N; i++) points[i].read();
sort(points + 1,points + 1 + N,cmpByX);
vector<Point> l;
vector<Point> r;
Point A = points[1];
Point B = points[N];
for(int i = 2;i <= N - 1; i++){
if(Cross(B - A,points[i] - A) > 0) l.push_back(points[i]);
if(Cross(B - A,points[i] - A) < 0) r.push_back(points[i]);
}
convex.push_back(A);
findConvex(A,B,l);
convex.push_back(B);
findConvex(B,A,r);
printf("%.2Lf\n",getPolygonPerimeter(convex));
}
int main(){
solve();
}
凸包问题是指在平面上找到能够包含所有给定点的最小凸多边形。
基本思想:
- 分解: 将点集按 x 坐标排序,并划分为左右两部分。
- 解决: 递归地找到左右两部分的凸包。
- 合并: 合并左右两部分的凸包,得到整体的凸包。
import java.util.Arrays;
import java.util.Stack;
public class ConvexHull {
static class Point implements Comparable<Point> {
int x, y;
Point(int x, int y) {
this.x = x;
this.y = y;
}
@Override
public int compareTo(Point p) {
return this.x != p.x ? this.x - p.x : this.y - p.y;
}
}
public static Point[] convexHull(Point[] points) {
Arrays.sort(points);
Stack<Point> lower = new Stack<>();
for (Point p : points) {
while (lower.size() >= 2 && cross(lower.get(lower.size() - 2), lower.get(lower.size() - 1), p) <= 0) {
lower.pop();
}
lower.push(p);
}
Stack<Point> upper = new Stack<>();
for (int i = points.length - 1; i >= 0; i--) {
Point p = points[i];
while (upper.size() >= 2 && cross(upper.get(upper.size() - 2), upper.get(upper.size() - 1), p) <= 0) {
upper.pop();
}
upper.push(p);
}
lower.pop();
upper.pop();
Point[] hull = new Point[lower.size() + upper.size()];
int k = 0;
for (Point p : lower) hull[k++] = p;
for (Point p : upper) hull[k++] = p;
return hull;
}
private static int cross(Point o, Point a, Point b) {
return (a.x - o.x) * (b.y - o.y) - (a.y - o.y) * (b.x - o.x);
}
public static void main(String[] args) {
Point[] points = { new Point(0, 3), new Point(2, 3), new Point(1, 1), new Point(2, 1), new Point(3, 0), new Point(0, 0), new Point(3, 3) };
Point[] hull = convexHull(points);
System.out.println("The points in the convex hull are:");
for (Point p : hull) {
System.out.println("(" + p.x + ", " + p.y + ")");
}
}
}
3. 时空权衡(Time-Space Tradeoff) #
时空权衡(Time-Space Tradeoff)是计算机科学中的一个重要概念,指的是在设计算法时,通过增加时间复杂度来减少空间复杂度,或者通过增加空间复杂度来减少时间复杂度。这个思想在许多算法设计中应用非常广泛,例如字符串匹配、B树和动态规划等。
时空权衡思想
时空权衡思想的基本原理是:在设计和优化算法时,可以在时间和空间之间做出选择和折中。例如,通过预处理数据并存储一些额外的信息,可以加快后续的查询速度;相反,减少存储空间则可能需要更复杂的计算过程来获得相同的结果。
应用实例
字符串匹配:
- 朴素算法:时间复杂度为 $O(nm)$,空间复杂度为 $O(1)$。
- KMP算法(Knuth-Morris-Pratt):通过预处理构建部分匹配表,时间复杂度为 $O(n + m)$,空间复杂度为 $O(m)$。
B树:
- B树是一种平衡树数据结构,适用于在磁盘或其他存储设备上进行大数据量的存储和快速检索。
- 通过增加树的阶数,B树减少了树的高度,从而减少了访问磁盘的次数,以换取更大的节点大小。
动态规划:
- 斐波那契数列:简单的递归算法时间复杂度为 $O(2^n)$,空间复杂度为 $O(n)$。
- 动态规划算法:通过存储子问题的解来避免重复计算,时间复杂度为 $O(n)$,空间复杂度可以是 $O(n)$ 或 $O(1)$(优化后的版本)。
示例 1:字符串匹配-Horpool算法



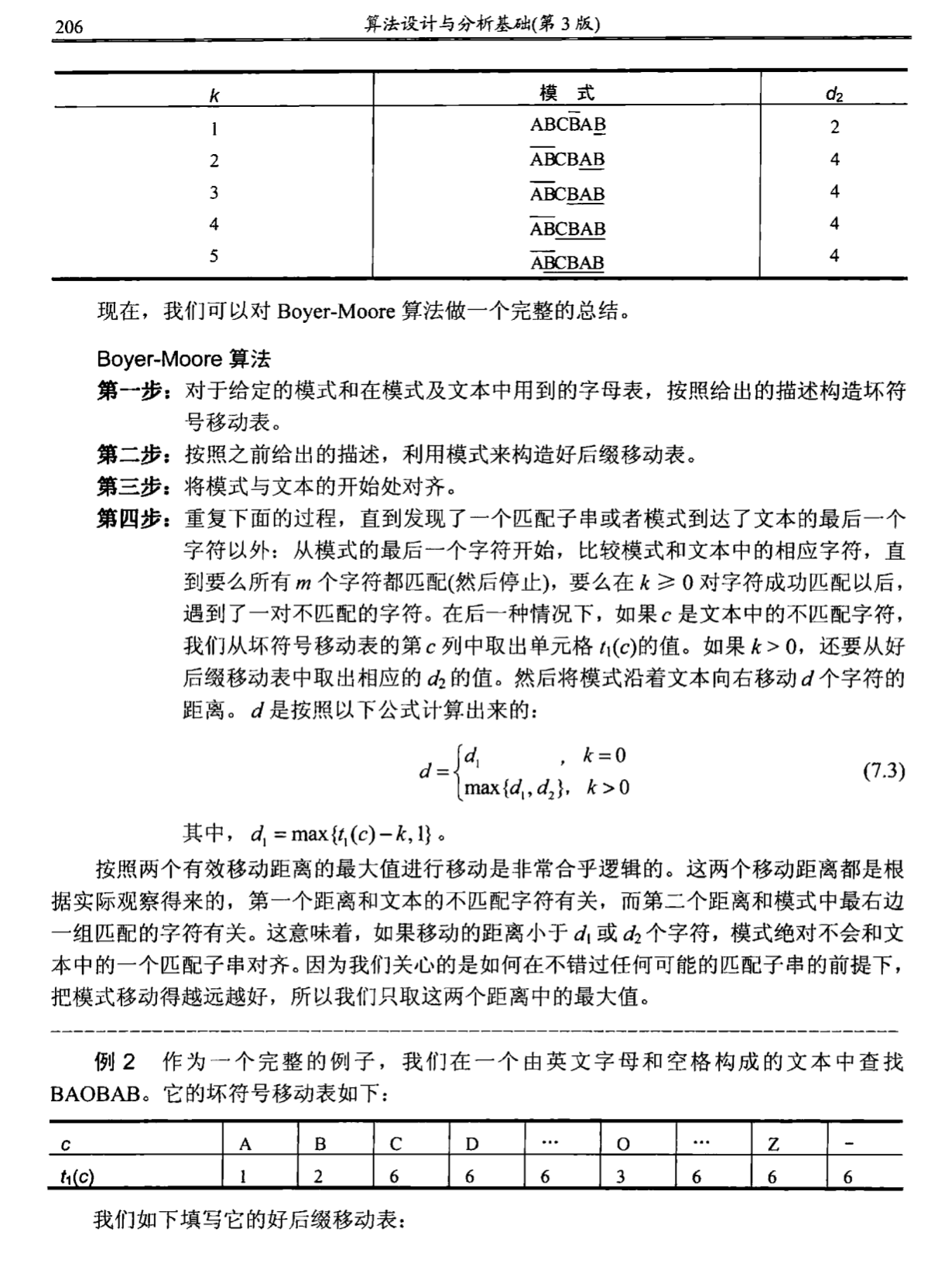
示例 2:Boyer-Moore 算法



示例 3:字符串匹配(KMP算法)


KMP算法是一种改进的字符串匹配算法,通过预处理模式串构建部分匹配表(也称为“前缀函数”),在匹配过程中避免不必要的比较,从而提高匹配效率。
public class KMP {
public static int[] computeLPSArray(String pattern) {
int m = pattern.length();
int[] lps = new int[m];
int length = 0;
int i = 1;
lps[0] = 0;
while (i < m) {
if (pattern.charAt(i) == pattern.charAt(length)) {
length++;
lps[i] = length;
i++;
} else {
if (length != 0) {
length = lps[length - 1];
} else {
lps[i] = 0;
i++;
}
}
}
return lps;
}
public static void KMPSearch(String text, String pattern) {
int n = text.length();
int m = pattern.length();
int[] lps = computeLPSArray(pattern);
int i = 0;
int j = 0;
while (i < n) {
if (pattern.charAt(j) == text.charAt(i)) {
i++;
j++;
}
if (j == m) {
System.out.println("Found pattern at index " + (i - j));
j = lps[j - 1];
} else if (i < n && pattern.charAt(j) != text.charAt(i)) {
if (j != 0) {
j = lps[j - 1];
} else {
i++;
}
}
}
}
public static void main(String[] args) {
String text = "ABABDABACDABABCABAB";
String pattern = "ABABCABAB";
KMPSearch(text, pattern);
}
}
示例 4:动态规划(斐波那契数列)
动态规划通过存储子问题的解来避免重复计算,提高算法效率。下面展示两种计算斐波那契数列的动态规划方法。
public class Fibonacci {
// 使用数组存储子问题的解
public static int fibDP(int n) {
if (n <= 1) {
return n;
}
int[] f = new int[n + 1];
f[0] = 0;
f[1] = 1;
for (int i = 2; i <= n; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
// 使用两个变量优化空间复杂度
public static int fibOptimized(int n) {
if (n <= 1) {
return n;
}
int a = 0, b = 1, c;
for (int i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return b;
}
public static void main(String[] args) {
int n = 10;
System.out.println("Fibonacci number using DP: " + fibDP(n));
System.out.println("Fibonacci number using optimized DP: " + fibOptimized(n));
}
}
示例 4:动态规划(币值最大化问题)

示例 5:动态规划(找零问题)

示例 6:动态规划(硬币收集问题)

4. 贪心部分 #
考点:
- 贪心法的思想和特点
- 特点:feasible、locally optimal、irrevocable
- 用贪心法解决经典问题:
- 活动相容问题和MST二选一;
- MST问题
- 不考察证明
- 掌握 Prim 或者 Kruskal 算法的算法过程
- 活动相容性问题
- 优化目标:安排的活动最多。先按结束时间排序,然后
- 不要求证明;需要掌握算法过程,选出对应活动。
- 可能要求写伪代码。
贪心法的思想和特点
贪心法(Greedy Algorithm)是一种在求解最优化问题时采用的策略。它通过在每一步都选择当前最优解(局部最优解),以期最终获得全局最优解。贪心法的思想和特点可以从以下几个角度进行介绍:
- Feasible(可行性):可行性指的是在每一步选择中,所选择的解必须满足问题的约束条件,即每一步选择都是合法的。例如,在找零钱问题中,每一步选择的硬币面值都必须是当前可以使用的硬币面值,这样最终能够凑出所需的总金额。
- Locally Optimal(局部最优):局部最优是贪心法的核心思想,即在每一个决策点上都选择当前看起来最好的选项,而不考虑未来的选择。这种策略依赖于以下假设:通过一系列局部最优的选择,最终能得到全局最优解。例如,在旅行推销员问题中,如果我们选择每一步都走向距离最近的未访问城市,这就是一种局部最优选择。
- Irrevocable(不可撤销性):不可撤销性意味着一旦在某一步做出了选择,就不能再回退或更改。贪心算法的这一特性要求在每一步选择时必须非常慎重,因为一旦选择了某个选项,就无法重新考虑之前的决策。例如,在最小生成树问题中的Prim算法或Kruskal算法中,一旦选择了一条边,就不会再撤销这个选择。
用贪心法解决经典问题
- 活动选择问题(Activity Selection Problem)
题目描述:给定一组活动,每个活动有一个开始时间和一个结束时间。你需要选择尽可能多的活动,使得它们互不重叠。活动的选择需要先按结束时间排序。
算法过程:
- 按活动的结束时间升序排序。
- 从第一个活动开始,选择结束时间最早且不与已选择活动重叠的活动。
伪代码:
活动选择(活动列表):
将活动列表按结束时间升序排序
选择第一个活动,并将其加入到已选择活动列表中
设定最后一个选择的活动的结束时间为第一个活动的结束时间
对于排序后活动列表中的每一个剩余活动:
如果 当前活动的开始时间 >= 最后一个选择的活动的结束时间:
选择当前活动
更新最后一个选择的活动的结束时间为当前活动的结束时间
返回已选择活动列表
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class ActivitySelection {
static class Activity {
int start;
int end;
Activity(int start, int end) {
this.start = start;
this.end = end;
}
}
public static List<Activity> selectActivities(Activity[] activities) {
Arrays.sort(activities, (a1, a2) -> a1.end - a2.end);
List<Activity> result = new ArrayList<>();
int lastEndTime = -1;
for (Activity activity : activities) {
if (activity.start >= lastEndTime) {
result.add(activity);
lastEndTime = activity.end;
}
}
return result;
}
public static void main(String[] args) {
Activity[] activities = {
new Activity(1, 4),
new Activity(3, 5),
new Activity(0, 6),
new Activity(5, 7),
new Activity(3, 9),
new Activity(5, 9),
new Activity(6, 10),
new Activity(8, 11),
new Activity(8, 12),
new Activity(2, 14),
new Activity(12, 16)
};
List<Activity> selectedActivities = selectActivities(activities);
System.out.println("Selected activities:");
for (Activity activity : selectedActivities) {
System.out.println("Activity: (" + activity.start + ", " + activity.end + ")");
}
}
}
- 最小生成树问题(Minimum Spanning Tree, MST)
使用Kruskal算法
题目描述:给定一个连通无向图,找到其最小生成树(MST)。即找到一个子图,使得所有节点连通且边的权重和最小。
Kruskal算法过程:
- 将图中的所有边按权重从小到大排序。
- 初始化一个空森林(每个节点都是一个单独的树)。
- 按权重从小到大依次检查每条边,如果加入该边不会形成环,则将该边加入MST。
import java.util.*;
public class KruskalMST {
static class Edge implements Comparable<Edge> {
int src, dest, weight;
public int compareTo(Edge compareEdge) {
return this.weight - compareEdge.weight;
}
}
static class Subset {
int parent, rank;
}
int V, E;
Edge[] edges;
KruskalMST(int v, int e) {
V = v;
E = e;
edges = new Edge[E];
for (int i = 0; i < e; ++i) {
edges[i] = new Edge();
}
}
int find(Subset[] subsets, int i) {
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
void union(Subset[] subsets, int x, int y) {
int xroot = find(subsets, x);
int yroot = find(subsets, y);
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
void KruskalMST() {
Edge[] result = new Edge[V];
int e = 0;
int i = 0;
for (i = 0; i < V; ++i)
result[i] = new Edge();
Arrays.sort(edges);
Subset[] subsets = new Subset[V];
for (i = 0; i < V; ++i)
subsets[i] = new Subset();
for (int v = 0; v < V; ++v) {
subsets[v].parent = v;
subsets[v].rank = 0;
}
i = 0;
while (e < V - 1) {
Edge next_edge = edges[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
if (x != y) {
result[e++] = next_edge;
union(subsets, x, y);
}
}
System.out.println("Following are the edges in the constructed MST");
for (i = 0; i < e; ++i)
System.out.println(result[i].src + " -- " + result[i].dest + " == " + result[i].weight);
}
public static void main(String[] args) {
int V = 4;
int E = 5;
KruskalMST graph = new KruskalMST(V, E);
graph.edges[0].src = 0;
graph.edges[0].dest = 1;
graph.edges[0].weight = 10;
graph.edges[1].src = 0;
graph.edges[1].dest = 2;
graph.edges[1].weight = 6;
graph.edges[2].src = 0;
graph.edges[2].dest = 3;
graph.edges[2].weight = 5;
graph.edges[3].src = 1;
graph.edges[3].dest = 3;
graph.edges[3].weight = 15;
graph.edges[4].src = 2;
graph.edges[4].dest = 3;
graph.edges[4].weight = 4;
graph.KruskalMST();
}
}
使用Prim算法
题目描述:同样是最小生成树问题,使用Prim算法来解决。Prim算法从一个顶点开始,不断扩展已选顶点集合,每次选择连接到已选顶点集合的权重最小的边。
Prim算法过程:
- 从一个起点开始,将该点加入MST集合。
- 重复以下过程,直到所有顶点都被包括在MST中:
- 在不形成环的前提下,从已选择的顶点集合中选出一条连接到未选顶点的最小边。
import java.util.*;
public class PrimMST {
private static final int V = 5;
int minKey(int[] key, Boolean[] mstSet) {
int min = Integer.MAX_VALUE, minIndex = -1;
for (int v = 0; v < V; v++) {
if (!mstSet[v] && key[v] < min) {
min = key[v];
minIndex = v;
}
}
return minIndex;
}
void printMST(int[] parent, int n, int[][] graph) {
System.out.println("Edge \tWeight");
for (int i = 1; i < V; i++)
System.out.println(parent[i] + " - " + i + "\t" + graph[i][parent[i]]);
}
void primMST(int[][] graph) {
int[] parent = new int[V];
int[] key = new int[V];
Boolean[] mstSet = new Boolean[V];
for (int i = 0; i < V; i++) {
key[i] = Integer.MAX_VALUE;
mstSet[i] = false;
}
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < V - 1; count++) {
int u = minKey(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++) {
if (graph[u][v] != 0 && !mstSet[v] && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
printMST(parent, V, graph);
}
public static void main(String[] args) {
PrimMST t = new PrimMST();
int[][] graph = new int[][]{
{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0}
};
t.primMST(graph);
}
}
5. 动态规划 #
考点:
- 动态规划的思想和特点
- 能写出问题分解为子问题的递归式(写出递归式就给大量分数)
- 能解决几个经典问题:
- LCS 最长公共子序列
- 序列:不连续、但是保持顺序的子集合。
- 序列 X、Y,找最长公共子序列 Z;
- 递归地从后往前面看;
- 回文子序列
- 矩阵连乘
- LCS 最长公共子序列
LCS:

回文子序列:DynamicProgrammingReview.pdf的P5 Problem 6

动态规划的思想:
动态规划(Dynamic Programming, DP)是一种通过将复杂问题分解为更小的子问题来解决复杂问题的算法技术。动态规划与分治法类似,但与分治法不同的是,动态规划会存储子问题的结果,从而避免重复计算。
动态规划的特点:
- 最优子结构:问题的最优解包含其子问题的最优解。
- 重叠子问题:子问题被多次重复计算。
- 子问题独立性:子问题间相互独立。
动态规划的经典问题
- 最长公共子序列(LCS)
问题描述:给定两个序列X和Y,找出它们的最长公共子序列Z。最长公共子序列是指在不改变序列相对顺序的前提下,从两个序列中选取的最长子序列。
递归式:
设$X$的长度为$m$,$Y$的长度为$n$,$dp[i][j]$表示$X$的前$i$个字符和$Y$的前$j$个字符的最长公共子序列长度。
- 如果$X[i-1] == Y[j-1]$,则$dp[i][j] = dp[i-1][j-1] + 1$
- 如果$X[i-1] != Y[j-1]$,则$dp[i][j] = max(dp[i-1][j], dp[i][j-1])$
public class LCS {
public static int longestCommonSubsequence(String X, String Y) {
int m = X.length();
int n = Y.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (X.charAt(i - 1) == Y.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
public static void main(String[] args) {
String X = "ABCBDAB";
String Y = "BDCAB";
System.out.println("最长公共子序列长度: " + longestCommonSubsequence(X, Y));
}
}
- 回文子序列
问题描述:给定一个字符串,找到它的最长回文子序列。回文子序列是指从左到右和从右到左都一样的子序列。
递归式:设字符串长度为$n$,$dp[i][j]$表示字符串从第$i$个字符到第$j$个字符的最长回文子序列长度。
- 如果$s[i] == s[j]$,则$dp[i][j] = dp[i+1][j-1] + 2$
- 如果$s[i] != s[j]$,则$dp[i][j] = max(dp[i+1][j], dp[i][j-1])$
public class LongestPalindromicSubsequence {
public static int longestPalindromeSubseq(String s) {
int n = s.length();
int[][] dp = new int[n][n];
for (int i = n - 1; i >= 0; i--) {
dp[i][i] = 1;
for (int j = i + 1; j < n; j++) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[n - 1][0];
}
public static void main(String[] args) {
String s = "bbbab";
System.out.println("最长回文子序列长度: " + longestPalindromeSubseq(s));
}
}
- 矩阵连乘问题
问题描述:给定一组矩阵,确定它们的相乘顺序,以使得乘积的计算代价最小。矩阵连乘问题中的计算代价由矩阵的维数决定。
递归式:设$dp[i][j]$表示从第$i$个矩阵到第$j$个矩阵的最小乘积计算代价,$p$为矩阵链的维数数组。
- $dp[i][j] = min(dp[i][k] + dp[k+1][j] + p[i-1]*p[k]*p[j]) (i ≤ k < j)$
public class MatrixChainMultiplication {
public static int matrixChainOrder(int[] p) {
int n = p.length - 1;
int[][] dp = new int[n][n];
for (int l = 2; l <= n; l++) {
for (int i = 0; i < n - l + 1; i++) {
int j = i + l - 1;
dp[i][j] = Integer.MAX_VALUE;
for (int k = i; k < j; k++) {
int q = dp[i][k] + dp[k + 1][j] + p[i] * p[k + 1] * p[j + 1];
if (q < dp[i][j]) {
dp[i][j] = q;
}
}
}
}
return dp[0][n - 1];
}
public static void main(String[] args) {
int[] p = {1, 2, 3, 4};
System.out.println("最小矩阵连乘计算代价: " + matrixChainOrder(p));
}
}
6. 平滑函数性质和主定理 #
6.1 平滑函数
平滑函数的背景:
- Complexity Analysis of BinCounting
$$ f(x)=[\frac{x}{2}] $$
希望把取整符号打开;
假设 $n=2^k$,那么$f(x)$就可以去掉取整符号,这时$f(x)$表达式看起来更舒服
我们希望这种良好的表达式不仅在数轴上的特殊点,而是把特殊点的性质扩展到数轴上;就需要用Smooth Function
- Smooth 函数
- 考点1:什么是Smooth Function(定义);说清楚 Smoothness Rule
- 考点2:Smooth函数有什么用?
- 考点3:某个函数是不是另一个函数的Smooth函数
类似判断题、概念题;
考点1:什么是 Smooth Function(定义)
定义:Smooth Function(光滑函数)通常是指在其定义域内具有连续导数(包括高阶导数)的函数。这意味着在数学上,光滑函数不仅是连续的,而且其导数也是连续的。通常,光滑函数可以在其定义域内进行无穷次微分。
在凸优化中,平滑函数是指具有一定光滑性(smoothness)的函数。具体来说,一个函数 $f(x)$ 被称为 $L$-平滑的($L$-smooth),如果它的梯度满足以下条件:
$$ [ |\nabla f(x) - \nabla f(y)| \leq L |x - y| ] $$
对所有 $x$ 和 $y$ 适用。这里,$L$ 是一个常数,称为 Lipschitz 常数,表示梯度变化的最大速率。
这个定义表明函数的梯度变化不会太剧烈,即梯度是 Lipschitz 连续的。这在优化算法中非常重要,因为它可以帮助我们理解和控制梯度的变化。
为什么需要定义平滑
定义平滑性主要是为了描述函数梯度的变化程度。在优化算法中,函数的梯度趋近于零意味着我们正在接近极小值点。平滑性可以帮助我们理解梯度在不同点之间的变化,这对于分析和设计优化算法非常有用。
平滑函数与凸性
我们有以下命题:
命题: 如果一个函数 $f(x)$ 是 $L$-平滑的,那么该函数是凸函数。
证明:
设 $f(x)$ 是 $L$-平滑的,定义函数 $g(x) = f(x) - \frac{L}{2} |x|^2$。
我们需要证明函数 $g(x)$ 是凸函数。为了证明这一点,我们需要证明 $g(x)$ 是单调的(即 $g(x)$ 的梯度是非递减的)。
计算 $g(x)$ 的梯度:
$$ [ \nabla g(x) = \nabla f(x) - Lx ] $$
接下来,我们检查 $g(x)$ 的二阶导数是否非负。即 Hessian 矩阵是否半正定:
$$ [ \nabla^2 g(x) = \nabla^2 f(x) - L I ] $$
其中 $I$ 是单位矩阵。
因为 $f(x)$ 是 $L$-平滑的,我们有:
$$ [ |\nabla f(x) - \nabla f(y)| \leq L |x - y| ] $$
这意味着 Hessian 矩阵的特征值不大于 $L$,即:
$$ [ \nabla^2 f(x) \preceq L I ] $$
因此,$\nabla^2 g(x) = \nabla^2 f(x) - L I \preceq 0$,即 Hessian 矩阵是负半定的。
这表明函数 $g(x)$ 是凸的。
根据函数 $g(x)$ 是凸函数,我们可以得到函数 $f(x)$ 的一个上界:
$$ [ f(y) \leq f(x) + \nabla f(x)^T (y - x) + \frac{L}{2} |y - x|^2 ] $$
这个上界对于后续分析优化算法的收敛性非常重要。
在公式
$$ [ |\nabla f(x) - \nabla f(y)| \leq L |x - y| ] $$
中,符号
$$ [ | \cdot | ] $$
表示向量的范数(norm),通常情况下是欧几里得范数(也称为二范数,L2范数)。以下是对范数的详细解释:
范数的定义
范数是一个函数,它将向量映射到非负实数,表示向量的“大小”或“长度”。常见的向量范数有几种类型:
欧几里得范数(L2范数):
定义:对于一个向量 $[ \mathbf{v} = (v_1, v_2, \ldots, v_n) ]$,其欧几里得范数定义为:$[ |\mathbf{v}|_2 = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2} ]$
也可以表示为:$[ |\mathbf{v}|2 = \sqrt{\sum{i=1}^n v_i^2} ]$
L1范数:
定义:对于一个向量 $[ \mathbf{v} = (v_1, v_2, \ldots, v_n) ]$,其L1范数定义为:$[ |\mathbf{v}|_1 = |v_1| + |v_2| + \cdots + |v_n| ]$
也可以表示为:$[ |\mathbf{v}|1 = \sum{i=1}^n |v_i| ]$
无穷范数(L∞范数):
定义:对于一个向量 $[ \mathbf{v} = (v_1, v_2, \ldots, v_n) ]$,其L∞范数定义为: $[ |\mathbf{v}|_\infty = \max { |v_1|, |v_2|, \ldots, |v_n| } ]$
公式中的范数
在公式 $[ |\nabla f(x) - \nabla f(y)| \leq L |x - y| ]$ 中,范数通常是指欧几里得范数(L2范数),除非另有说明。这是因为欧几里得范数在优化和梯度计算中最为常用。具体来说:
$[ |\nabla f(x) - \nabla f(y)| ]$ 表示梯度向量 $[ \nabla f(x) ]$ 和 $[ \nabla f(y) ]$ 之间的欧几里得距离(即梯度差的长度)。
$[ |x - y| ]$ 表示点 $[ x ]$ 和 $[ y ]$ 之间的欧几里得距离(即坐标差的长度)。
Smoothness Rule:光滑函数的一个基本规则是:一个函数 $f(x)$ 被称为是光滑的,当且仅当它在其定义域内的所有阶导数都存在且连续。
形式化定义:如果 $f(x)$ 在区间 $[a, b]$ 内的任意点处都具有任意阶的连续导数,则称 $f(x)$ 是区间 $[a, b]$ 上的光滑函数。
考点2:Smooth函数有什么用?
光滑函数在数学和工程中有许多重要的应用,主要包括以下几个方面:
- 简化计算和分析:在某些情况下,我们需要对离散或不连续的函数进行处理。例如,在复杂性分析中,处理取整符号(如 $\left\lfloor \frac{x}{2} \right\rfloor$)的函数可能比较麻烦。通过用光滑函数进行近似,可以简化计算和分析。
- 信号处理:在信号处理中,光滑函数用于平滑数据,消除噪声。通过将不规则的数据转换为平滑的曲线,可以更容易地分析数据的趋势和模式。
- 数值分析和优化:在数值分析和优化问题中,光滑函数用于确保函数在迭代过程中具有良好的数值稳定性。光滑函数有助于避免不稳定的数值行为,并且在求解最优化问题时可以提高收敛速度。
- 计算机图形学:在计算机图形学中,光滑函数用于生成光滑的曲面和曲线,使图形渲染更加平滑和逼真。
考点3:某个函数是不是另一个函数的 Smooth 函数
要判断一个函数是否是另一个函数的光滑函数,我们通常需要检查以下几个方面:
- 连续性:检查函数是否在其定义域内是连续的。
- 导数的存在性和连续性:检查函数的导数是否存在,并且导数在定义域内是否也是连续的。如果是高阶光滑函数,则需要检查所有阶导数的连续性。
- 近似性:如果一个函数 $g(x)$ 是 $f(x)$ 的光滑版本,则 $g(x)$ 应该在定义域内良好地近似 $f(x)$。这意味着对于所有 $x$,$g(x)$ 应该尽可能接近 $f(x)$,并且这种近似在函数的导数上也是成立的。
示例
例子:处理取整符号的光滑函数
考虑函数 $f(x) = \left\lfloor \frac{x}{2} \right\rfloor$。为了去掉取整符号,我们希望找到一个光滑函数来近似它。
假设 $n = 2^k$,那么 $f(x) = \left\lfloor \frac{x}{2} \right\rfloor$ 可以去掉取整符号,因为在这些点上 $x$ 是 2 的整数倍,因此取整符号对结果没有影响。
为了将这种性质扩展到整个数轴上,我们可以使用一个光滑函数来近似它,例如:
$$ [ g(x) = \frac{x}{2} - \frac{1}{2} \sin\left(2\pi \frac{x}{2}\right) ] $$
在这种情况下,$g(x)$ 是 $\left\lfloor \frac{x}{2} \right\rfloor$ 的一个光滑近似,它在所有点上都是连续和可微的。
验证:
- 连续性:$g(x)$ 在整个定义域内是连续的。
- 导数的存在性和连续性:$g(x)$ 的导数存在并且是连续的。
- 近似性:对于所有 $x$,$g(x)$ 都接近于 $\left\lfloor \frac{x}{2} \right\rfloor$。
因此,$g(x)$ 是 $\left\lfloor \frac{x}{2} \right\rfloor$ 的一个光滑近似函数。
6.2 分治法和主定理

解方程 $T(n)=bT(n/c)+f(n)$
- 不用背别的;就用Master Theorem就行
- 判断满足主定理的哪一条,算一下case 1、case2、case3,然后代入主定理的结论就行;
- T(n)=9T(n/3)+n
- 有3个辅助量;D、E、L
- 03-Recursion.ppt:


分治法和主定理
分治法(Divide and Conquer)是一种常用的算法设计范式,其基本思想是将一个复杂的问题分解为若干个规模较小的子问题,递归地求解这些子问题,然后将子问题的解合并得到原问题的解。
主定理(Master Theorem)
主定理是用来分析分治算法时间复杂度的一种工具。它适用于以下形式的递归方程:
$$ [ T(n) = aT\left(\frac{n}{b}\right) + f(n) ] $$
其中:
- $a \geq 1$ 表示每次递归调用产生的子问题数。
- $b > 1$ 表示子问题规模缩减的因子。
- $f(n)$ 是分解和合并所需的时间。
主定理将递归方程的解分为三种情况:
-
情况 1: 如果 $f(n) = O(n^c)$ 且 $c < \log_b a$,则 $[ T(n) = \Theta(n^{\log_b a}) ]$
-
情况 2: 如果 $f(n) = \Theta(n^c)$ 且 $c = \log_b a$,则 $[ T(n) = \Theta(n^c \log n) ]$
-
情况 3: 如果 $f(n) = \Omega(n^c)$ 且 $c > \log_b a$,并且满足正则性条件 $af\left(\frac{n}{b}\right) \leq kf(n)$ 对于某个常数 $k < 1$ 和足够大的 $n$,则 $[ T(n) = \Theta(f(n)) ]$
示例:合并排序(Merge Sort)
合并排序是一种典型的分治算法,其时间复杂度可以通过主定理来分析。
合并排序的递归方程:
$$ [ T(n) = 2T\left(\frac{n}{2}\right) + O(n) ] $$
- $a = 2$:每次递归产生两个子问题。
- $b = 2$:每个子问题的规模是原问题的一半。
- $f(n) = O(n)$:合并两个子问题所需的时间。
应用主定理:
-
计算 $\log_b a$: $[ \log_2 2 = 1 ]$
-
对比 $f(n)$ 和 $n^{\log_b a}$:
- $f(n) = O(n)$
- $n^{\log_b a} = n^1 = n$
因为 $f(n) = \Theta(n)$ 和 $n^{\log_b a} = n$,这符合主定理的第二种情况。
结论:
根据主定理的第二种情况: $$ [ T(n) = \Theta(n \log n) ] $$
另一个示例:二分查找(Binary Search)
二分查找是一种经典的分治算法,用于在排序数组中查找元素,其时间复杂度也可以通过主定理来分析。
二分查找的递归方程:
$$ [ T(n) = T\left(\frac{n}{2}\right) + O(1) ] $$
- $a = 1$:每次递归产生一个子问题。
- $b = 2$:子问题的规模是原问题的一半。
- $f(n) = O(1)$:分解和合并所需的时间是常数时间。
应用主定理:
-
计算 $\log_b a$: [ \log_2 1 = 0 ]
-
对比 $f(n)$ 和 $n^{\log_b a}$:
- $f(n) = O(1)$
- $n^{\log_b a} = n^0 = 1$
因为 $f(n) = \Theta(1)$ 和 $n^{\log_b a} = 1$,这符合主定理的第二种情况。
结论:
根据主定理的第二种情况: [ T(n) = \Theta(\log n) ]
7. 复杂度表示法 #
考点:
$O(f)$、$\Omega (f)$、$\Theta (f)$的性质
- 考点1:三个性质是什么含义;(用Definition、极限或者自然语言描述)
- 考点2:性质transitive、对称性和properties这两页;

大O记号($O(f)$)、大Ω记号($\Omega(f)$)、大Θ记号($\Theta(f)$)的性质
考点1:三个性质的含义
- 大O记号($O(f)$)
Definition: 对于两个函数 $f(n)$ 和 $g(n)$,如果存在正整数 $c$ 和 $n_0$,使得当 $n \ge n_0$ 时,$0 \le f(n) \le c \cdot g(n)$,则称 $f(n)$ 是 $g(n)$ 的大O记号,记作 $f(n) = O(g(n))$。
极限描述:
$$ f(n) = O(g(n)) \iff \lim_{n \to \infty} \frac{f(n)}{g(n)} \le C \quad (C \text{为常数}) $$
自然语言描述: $f(n)$ 的增长速度最多和 $g(n)$ 的增长速度一样快(或更慢)。
- 大Ω记号($\Omega(f)$)
Definition: 对于两个函数 $f(n)$ 和 $g(n)$,如果存在正整数 $c$ 和 $n_0$,使得当 $n \ge n_0$ 时,$0 \le c \cdot g(n) \le f(n)$,则称 $f(n)$ 是 $g(n)$ 的大Ω记号,记作 $f(n) = \Omega(g(n))$。
极限描述:
$$ f(n) = \Omega(g(n)) \iff \lim_{n \to \infty} \frac{f(n)}{g(n)} \ge C \quad (C \text{为常数}) $$
自然语言描述: $f(n)$ 的增长速度至少和 $g(n)$ 的增长速度一样快(或更快)。
- 大Θ记号($\Theta(f)$)
Definition: 对于两个函数 $f(n)$ 和 $g(n)$,如果存在正整数 $c_1, c_2$ 和 $n_0$,使得当 $n \ge n_0$ 时,$0 \le c_1 \cdot g(n) \le f(n) \le c_2 \cdot g(n)$,则称 $f(n)$ 是 $g(n)$ 的大Θ记号,记作 $f(n) = \Theta(g(n))$。
极限描述:
$$ f(n) = \Theta(g(n)) \iff \lim_{n \to \infty} \frac{f(n)}{g(n)} = C \quad (C \text{为常数}) $$
自然语言描述: $f(n)$ 的增长速度和 $g(n)$ 的增长速度一样快(同阶)。
考点2:性质transitive、对称性和properties
- Transitive(传递性)
- 大O记号: 如果 $f(n) = O(g(n))$ 且 $g(n) = O(h(n))$,则 $f(n) = O(h(n))$。
- 大Ω记号: 如果 $f(n) = \Omega(g(n))$ 且 $g(n) = \Omega(h(n))$,则 $f(n) = \Omega(h(n))$。
- 大Θ记号: 如果 $f(n) = \Theta(g(n))$ 且 $g(n) = \Theta(h(n))$,则 $f(n) = \Theta(h(n))$。
- 对称性
-
大O记号: 大O记号没有对称性,即 $f(n) = O(g(n))$ 并不意味着 $g(n) = O(f(n))$。
-
大Ω记号: 大Ω记号没有对称性,即 $f(n) = \Omega(g(n))$ 并不意味着 $g(n) = \Omega(f(n))$。
-
大Θ记号: 大Θ记号具有对称性,即 $f(n) = \Theta(g(n))$ 意味着 $g(n) = \Theta(f(n))$。
- Properties(其他性质)
-
大O记号的性质:
- 如果 $f_1(n) = O(g_1(n))$ 且 $f_2(n) = O(g_2(n))$,则 $f_1(n) + f_2(n) = O(\max(g_1(n), g_2(n)))$。
- 如果 $f(n) = O(g(n))$ 且 $g(n) = O(h(n))$,则 $f(n) = O(h(n))$(传递性)。
- 如果 $c$ 是常数,且 $f(n) = O(g(n))$,则 $c \cdot f(n) = O(g(n))$。
-
大Ω记号的性质:
- 如果 $f_1(n) = \Omega(g_1(n))$ 且 $f_2(n) = \Omega(g_2(n))$,则 $f_1(n) + f_2(n) = \Omega(\min(g_1(n), g_2(n)))$。
- 如果 $f(n) = \Omega(g(n))$ 且 $g(n) = \Omega(h(n))$,则 $f(n) = \Omega(h(n))$(传递性)。
- 如果 $c$ 是常数,且 $f(n) = \Omega(g(n))$,则 $c \cdot f(n) = \Omega(g(n))$。
-
大Θ记号的性质:
- 如果 $f_1(n) = \Theta(g_1(n))$ 且 $f_2(n) = \Theta(g_2(n))$,则 $f_1(n) + f_2(n) = \Theta(\max(g_1(n), g_2(n)))$。
- 如果 $f(n) = \Theta(g(n))$ 且 $g(n) = \Theta(h(n))$,则 $f(n) = \Theta(h(n))$(传递性)。
- 如果 $c$ 是常数,且 $f(n) = \Theta(g(n))$,则 $c \cdot f(n) = \Theta(g(n))$。
8. NPC #

- 考点1:NPC的定义是什么?介绍NPC理论;P、NP、NPC
- 含义和实际应用场景;发现一个NPC问题;
- 考点2:列举一些NPC问题
- 子集和问题
- 哈米尔顿图、哈米尔顿回路
- 01背包
- 装箱问题
- 考点3:怎么证装箱问题和01背包是NPC问题
- 首先证明NP,写NP算法;
- step1:猜测;genCertificate()这一步;猜k次;包含k个点的组合;并行多道;O(1)时间;
- step2:验证;任意两个点之间都有边,就是完全子图;
- 如果满足条件,输出yes
- 然后证明它们是NP Hard 问题
- (没听懂老师说的)能不能用另一个NP定义?多项式时间内验证、证明,找完全子图;blablabla… 也是可以的
- 首先证明NP,写NP算法;
- 如何证明装箱问题和01背包是NP Hard 问题?
- 会给这样给题目:已知装箱问题是NP Hard 问题,请你给出多项式规约,证明 01背包和装箱问题其实是等价的,因此01背包是NP Hard 问题
- 证明过程后续会在moodle上给出详细的pdf资料,认真看就行。
- 多项式规约的含义?规约=证明问题等价。多项式规约意思是我们能用一个多项式时间复杂度的算法,将问题A的输入和约束转换为已解决问题B的输入和约束。这个转换过程就是多项式规约。
P、NP、NPC 含义及实际应用场景
-
P 类问题(Polynomial time problems)
- 含义:可以在多项式时间内(即时间复杂度为多项式函数)由确定性图灵机解决的问题。
- 应用场景:许多常见的计算问题,如排序(例如快速排序、归并排序)、搜索(例如二分搜索)等。
-
NP 类问题(Non-deterministic Polynomial time problems)
- 含义:如果一个问题的解可以在多项式时间内由确定性图灵机验证,非确定性图灵机求解,则该问题属于 NP 类。
- 应用场景:许多复杂的决策和优化问题,如旅行商问题(TSP)、着色问题等。
-
NPC 类问题(NP-Complete problems)
- 含义:如果一个问题既属于 NP 类,又是 NP 难的(NP-Hard),则称该问题为 NP 完全问题(NPC)。NP 完全问题是最难的 NP 类问题。
- 应用场景:包括许多实际中的复杂问题,如工作调度、资源分配、网络设计等。
NPC 理论
NPC 理论研究的是问题的计算复杂性,特别是关于问题的可计算性和计算难度。对于一个给定的 NP 完全问题,如果能找到一个多项式时间算法来解决它,那么所有的 NP 问题都可以在多项式时间内解决。这就是著名的 P=NP 问题。
发现一个 NPC 问题
发现一个新的 NPC 问题通常涉及两个步骤:
- 证明问题属于 NP 类:需要展示一个多项式时间内验证解的算法。
- 证明问题是 NP 难的(NP-Hard):需要找到一个已知的 NPC 问题,并通过多项式时间规约(Polynomial-time reduction)将其转化为该问题。
考点2:列举一些 NPC 问题
子集和问题(Subset Sum Problem)
- 描述:给定一个整数集合和一个目标值,确定是否存在一个子集,其元素和等于目标值。
哈米尔顿图、哈米尔顿回路(Hamiltonian Path and Cycle)
- 描述:给定一个图,确定是否存在一条经过每个顶点一次的路径(哈米尔顿路径)或回路(哈米尔顿回路)。
01 背包问题(0/1 Knapsack Problem)
- 描述:给定一组物品,每个物品有重量和价值,在总重量不超过容量的情况下,选择一些物品使得总价值最大。
装箱问题(Bin Packing Problem)
- 描述:给定一组物品和若干个固定容量的箱子,确定如何将物品装入箱子,使得使用的箱子数最少。
考点3:证明装箱问题和 01 背包问题是 NPC 问题


装箱问题
- 首先证明 NP
- 猜测:生成一个可能的物品分配方案,即猜测每个物品放在哪个箱子里。
- 验证:检查每个箱子的总重量是否不超过容量。如果所有箱子的重量都符合要求,输出“是”;否则,输出“否”。
- 证明 NP-Hard
- 假设有一个已知的 NP 完全问题,如子集和问题。通过多项式时间规约,将子集和问题转换为装箱问题。
- 为了证明装箱问题和 01 背包问题是 NP-Hard,需要进行多项式规约。
- 证明装箱问题是 NP-Hard:假设装箱问题是 NP-Hard。将装箱问题转化为 01 背包问题,展示如何使用装箱问题的解来解决 01 背包问题。
01 背包问题
- NP 证明:
- 猜测:生成一个可能的物品选择方案,即猜测每个物品是否被选择。
- 验证:检查选择的物品总重量是否不超过容量,并计算总价值。如果总重量符合要求且总价值达到最大,输出“是”;否则,输出“否”。
- 证明 NP-Hard
- 为了证明装箱问题和 01 背包问题是 NP-Hard,需要进行多项式规约。
9. 近似算法 #
推荐下面的博文
-
考点1:近似算法的定义和如何衡量近似算法的好坏?
-
考点2:掌握几种装箱问题的贪心算法;(FF、NF等)
具体:
- 近似定理:
- 求最小还是最大,始终让近似比大于等于1
- 让算法的比值越小越接近1,近似精度越好;否则相反;
- 不管证明;搞懂3种过程(都是贪心)
- NF算法 Next Fit
- 放不放得下?
- 放得下。放进箱子。
- 放不下,来个新箱子。
- O(n)
- 只看当前箱子
- 放不放得下?
- FF算法 First Fit
- 从第一个箱子开始判断,会遍历前面的箱子;
- 放不放得下?
- 放得下。放进箱子。
- 放不下,来个新箱子。
- O(nm)约等于O(n^2)
- 放不放得下?
- 从第一个箱子开始判断,会遍历前面的箱子;
- FFD算法:先把所有元素排序;然后尽可能装最大的
- 伪代码:先写排序;
- 箱子大小是单位1;
- for-i for-j;i是物品;j是箱子;
- O(ilogi);O(ij)
- 不是在线算法;因为输入已经结束了,知道了所有输入;
- 3个算法哪个是/不是在线算法?复杂度如何?
- FFD不是在线算法,其他都是;因为FFD要做排序,做了排序就不是在线算法了(相当于你已经看过所有数据了,即数据输入已经结束了,在线算法意思是要实时接收算法输入)
考点1:近似算法的定义和如何衡量近似算法的好坏?
- 近似算法定义:对于某些NP完全问题,近似算法能在多项式时间内给出一个可行解,但该解可能不是最优解。近似算法的输出是输入实例的一个近似解,通常使用多项式时间完成。
- 衡量标准:近似算法的好坏通过“近似比”(Approximation Ratio)来衡量。对于最小化问题,近似比定义为算法得到的解与最优解的比值的最大可能值。理想情况下,这个比值接近1,表示近似解非常接近最优解。
考点2:掌握几种装箱问题的贪心算法(FF、NF等)



NF算法(Next Fit):
- 策略:始终尝试将新物品放入当前打开的箱子中。如果放不下,则开一个新的箱子。
- 时间复杂度:O(n),因为它只检查当前的箱子。
- 特点:是一个在线算法,因为它不需要知道所有的输入。
FF算法(First Fit):
- 策略:从第一个箱子开始尝试,依次检查每个已打开的箱子,看是否能放入当前物品。如果所有箱子都放不下,开一个新的箱子。
- 时间复杂度:O(nm),约等于O(n^2)(m为箱子数量)。
- 特点:也是一个在线算法,因为处理每个物品只依赖之前的箱子状态。
FFD算法(First Fit Decreasing):
- 策略:先将所有物品按大小降序排序,然后使用FF算法尝试装箱。
- 时间复杂度:O(n log n)(排序)和O(nm)(装箱),总体约O(n^2)。
- 特点:不是一个在线算法,因为需要在处理前先看到所有的物品来进行排序。
在这三种算法中,FFD算法虽然在处理前需要所有数据(因此不是在线算法),但通常能提供更好的装箱效率。FF和NF都是在线算法,能够逐个处理输入数据,但在最坏情况下它们的表现可能不如FFD算法。
