Online Learning是工业界比较常用的机器学习算法,在很多场景下都能有很好的效果。
机器学习纯粹主义者可能会嘲笑实时学习在线算法的想法。训练模型可能会以多种不同的方式出现错误:算法本身可能不合适,模型可能无法很好地泛化,学习率可能错误,正则化可能太低或太高……这样的例子不胜枚举。当无法保证会发生什么时,我们到底为什么要尝试立即学习?
答案很简单:无论模型有多好,或者输入了多少数据,模型仍然是环境的不完美表示。为了立即做出最佳决策,我们不能拥有一个只知道昨天发生的事情的模型。
import numpy as np
from sklearn import linear_model
n_samples, n_features = 1, 500
y = np.random.randn(n_samples)
X = np.random.randn(n_samples, n_features)
clf = linear_model.SGDRegressor()
# 该fit()方法完成了所有的训练魔法,产生了一个我们可以用于预测的模型
clf.fit(X, y)
import time
start_time = time.time()
# 还有一种partial_fit()方法,可以对小批量数据进行增量训练。
clf.partial_fit(X, y)
elapsed_time = time.time() - start_time
print(elapsed_time)
Online Learning(也称增量学习或核外学习)并不是一种模型,而是一种模型的训练方法,Online Learning能够根据线上反馈数据,实时快速地进行模型调整,使得模型及时反映线上的变化,提高线上预测的准确率。Online Learning的流程包括:将模型的预测结果展现给用户,然后收集用户的反馈数据,再用来训练模型,形成闭环的系统。如下图所示:
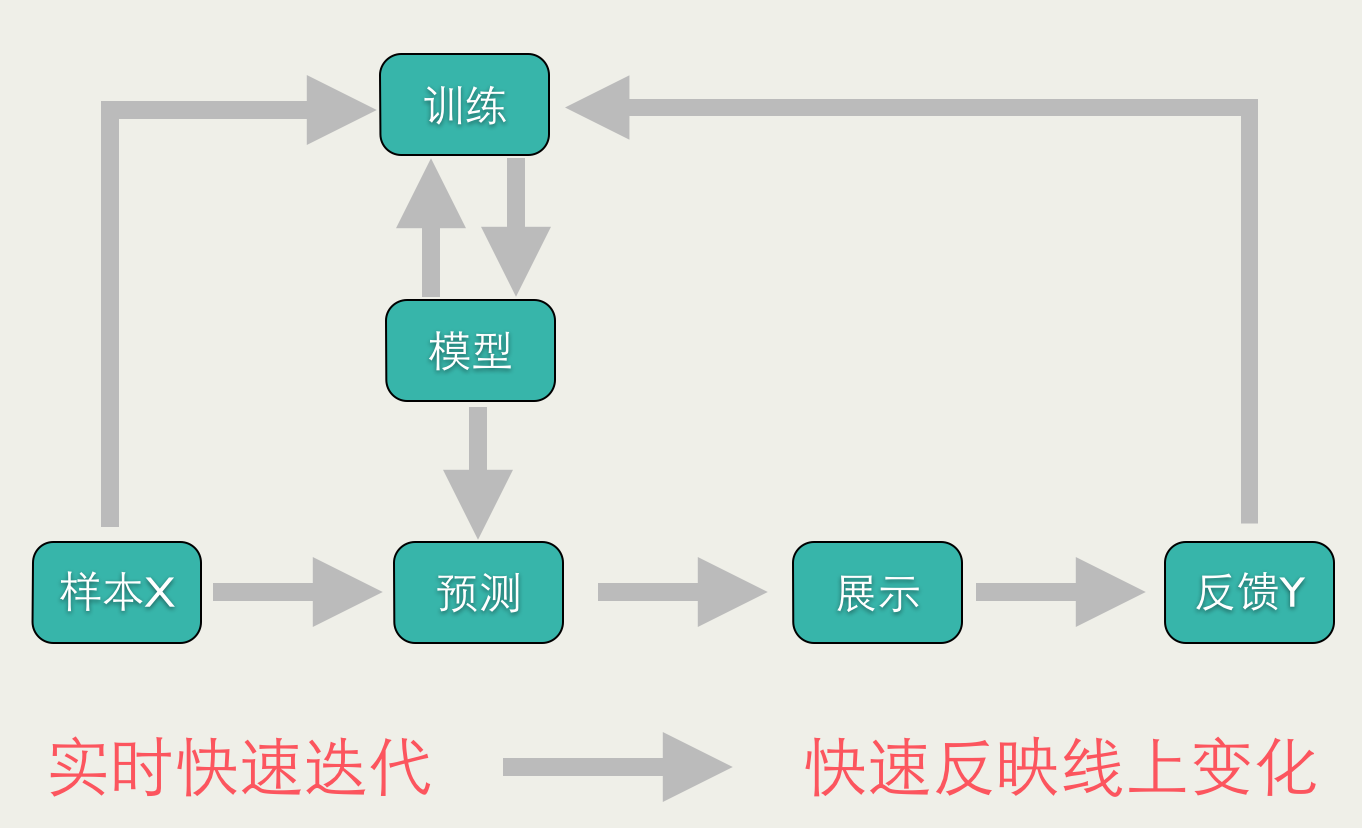
Online Learning有点像自动控制系统,但又不尽相同,二者的区别是:Online Learning的优化目标是整体的损失函数最小化,而自动控制系统要求最终结果与期望值的偏差最小。
传统的训练方法,模型上线后,更新的周期会比较长(一般是一天,效率高的时候为一小时),这种模型上线后,一般是静态的(一段时间内不会改变),不会与线上的状况有任何互动,假设预测错了,只能在下一次更新的时候完成更正。Online Learning训练方法不同,会根据线上预测的结果动态调整模型。如果模型预测错误,会及时做出修正。因此,Online Learning能够更加及时地反映线上变化。
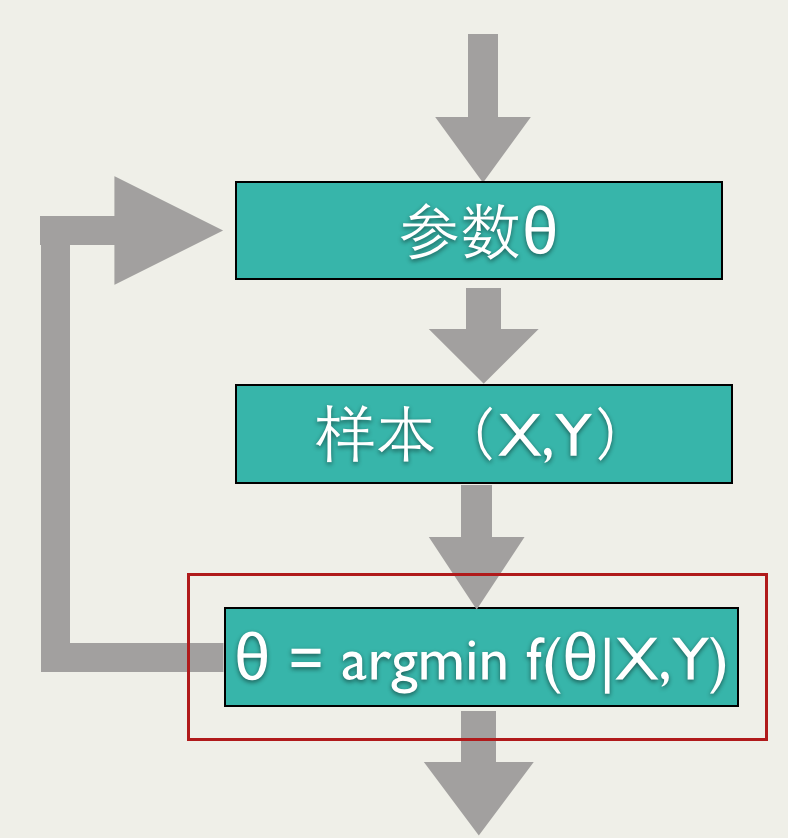
如上图所示,Online Learning训练过程也需要优化一个目标函数(红框标注的),但是和其他的训练方法不同,Online Learning要求快速求出目标函数的最优解,最好是能有解析解。
Online Learning 的实现方法 #
前面说到Online Learning要求快速求出目标函数的最优解。要满足这个要求,一般的做法有两种:
- FTRL(Follow The Regularized Leader)
- BPR(Bayesian Probit Regression)
McMahan H B, Holt G, Sculley D, et al. Ad Click Prediction: a View from the Trenches. Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD). 2013.
Graepel T, Candela J Q, Borchert T,et al. Web-Scale Bayesian Click-Through Rate Prediction for Sponsored Search Advertising in Microsoft’s Bing Search Engine. Proceedings of the 27th International Conference on Machine Learning ICML. 2010.
下面就详细介绍这两种做法的思路。
Bayesian Online Learning #
贝叶斯方法能够比较自然地导出Online Learning的训练方法:给定参数先验,根据反馈计算后验,将其作为下一次预测的先验,然后再根据反馈计算后验,如此进行下去,就是一个Online Learning的过程,如下图所示。
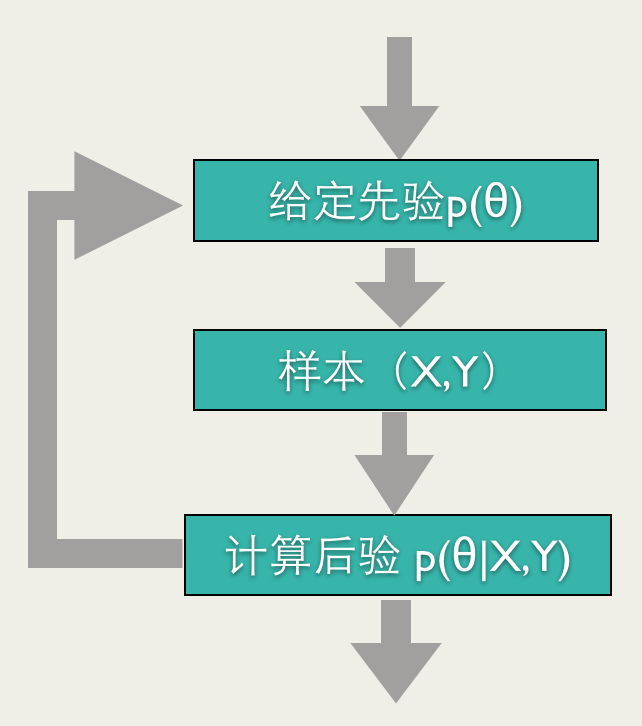
举个例子, 我们做一个抛硬币实验,估算硬币正面的概率 $\mu$ 。我们假设 $\mu$ 的先验满足 $p(\mu)=Beta(\alpha,\beta)$ 。
- 对于观测值 $Y=1$ ,代表是正面,我们可以算的后验 $p(\mu | Y=1)=Beta(\alpha +1,\beta)$
- 对于观测值 $Y=0$ ,代表是反面,我们可以算的后验 $p(\mu | Y=0)=Beta(\alpha,\beta + 1)$
补充 Beta分布
