4.1 分类简介及其与回归的区别 #
分类模型应用案例(Classification Cases) #
- 信用评分(Credit Scoring)
- 输入:收入、储蓄、职业、年龄、信用历史等等
- 输出:是否贷款
- 医疗诊断(Medical Diagnosis)
- 输入:现在症状、年龄、性别、病史
- 输出:哪种疾病
- 手写文字识别(Handwritten Character Recognition)
- 输入:文字图片
- 输出:是哪一个汉字
- 人脸识别(Face Recognition)
- 输入:面部图片
- 输出:是哪个人
把分类当成回归去做 #
不行
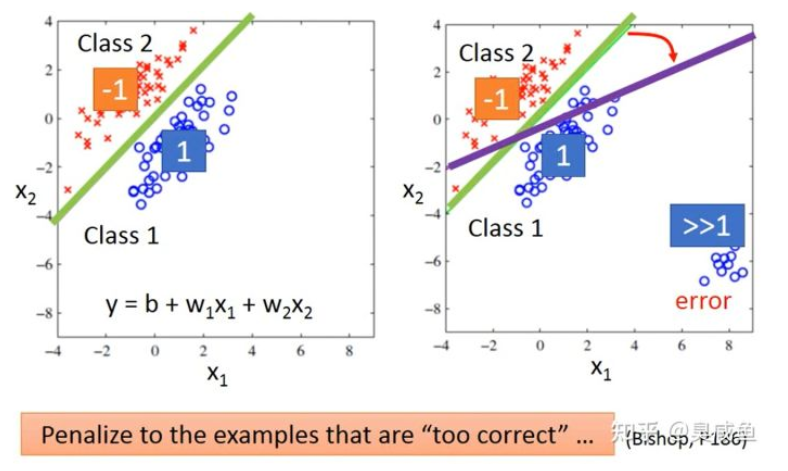
- 假设有两个类别,其中类别1的标签为1,类别2的标签为-1,那0就是分界线,大于0就是类别1,小于0就是类别2。但是回归模型会惩罚哪些太正确的样本,如果结果远远大于1,它的分类应该是类别1还是类别2?这时为了降低整体误差,需要调整已经找到的回归函数,就会导致结果的不准确。
-
- 假设有多个类别,类别1的标签是1,类别2的标签是2,类别3的标签是3。这样的话,标签间具有2和3相近、3大于2这种本来不存在的数字关系。
理想替代方案(Ideal Alternatives) #
- 模型:模型可以根据特征判断类型,输入是特征,输出是类别
- 损失函数:预测错误的次数,即$L(f)=\sum_n{\sigma(f(x_n) \neq \hat{y_n}) }$ 。这个函数不可微。
- 如何找到最好的函数,比如感知机(Perceptron)、支持向量机(SVM)
4.2 分类模型指概率生成模型 #
贝叶斯公式 #
- $P(A \cap B) = P(A)P(B|A) = P(B)P(A|B)$
- $P(A|B) = \frac{P(A)P(B|A)}{P(B)}$
全概率公式 #
$P(B)=\sum_{i=1}^{n}{P(A_i)P(B|A_i)}$
概率生成模型(Probalitity Genetative Model) #
理论与定义 #
假设有两个类别的$C_1和C_2$,要判断对象$x$属于哪个类别,这样把分类问题变成了概率计算问题。
- 根据贝叶斯公式(Bayes’ theorem)和全概率公式(Total Probability Theorem)可以知道,$x$属于类别$C_1$的概率为$P(C_1|x)= \frac{P(x|C_1)P(C_1)}{P(x)}=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}$ ,如果$P(C_1|x)>0.5$ 则类别为$C_1$ ,否则类别为$C_2$。
- 概率生成模型的意思就是可以通过这个模型生成一个$$x$$。具体来讲就是,根据$P(x)=P(x|C_1)P(C_1)+P(x|C_2)P(C_2)$ 计算出$P(x)$,就可以知道 $x$ 的分布进而生成 $x$ 。如果想要计算出$P(x)$,就要根据训练集估计出$P(C_1)$、$P(x|C_1)$、$P(C_2)$、$P(x|C_2)$这四个值。更直观一点地讲,每个类别就是一个多元正态分布,其中多元是因为每个样本有多个维度的特征。
- 可以根据数据集中属于两个类别的对象的数量计算 $P(C_1)$ 和 $P(C_2)$ 这两个先验概率(Prior Probability)。如果有2个样本属于类别$C_1$ ,4个样本属于类别$C_2$ ,那$P(C_1)= \frac{1}{3}$、$P(C_2)= \frac{2}{3}$。
- 要计算后验概率(Posterior Probability)$P(x|C_1)$ 和 $P(x|C_2)$,可以假设训练集中的各类别样本的特征分别是从某个多元正太分布(多元对应特征的多维)中取样得到的,或者说是假设训练集中各类别样本的特征分别符合某多元正态分布。该正太分布的输入是一个样本的特征 $x$,输出为样本 $x$ 是从这个正太分布取样得到(或者说该样本属于某类别)的概率密度,然后通过积分就可以求得 $P(x|C_1)$ 和 $P(x|C_2)$ 。
- 正太分布公式为 $f_{\mu,\sum{(x)}}=\frac{1}{(2\pi)^\frac{D}{2}} \frac{1}{|\sum|^\frac{1}{2}} {e^{-\frac{1}{2}(x-\mu)^T\sum^{-1}{x-\mu}}}$ 。正太分布有2个参数,即均值 $\mu$ (代表正太分布的中心位置)和协方差矩阵(Covariance Matrix)$\sum$ (代表正态分布的离散程度),计算出均值 $\mu$ 和协方差 $\sum$ 即可得到该正态分布。公式中的 $D$ 为多维特征的维度。
- 实际上从任何一个正态分布中取样都有可能得到训练集中的特征,只是概率不同而已。通过极大值似然估计(Maximum Likelihood Estimate,MLE),我们可以找到取样得到训练集特征的概率最大的那个正态分布,假设其均值和协方差矩阵为 $ \mu^* $ 和 $ \sum^* $ 。
- 根据某正态分布的均值 $\mu$ 和协方差 $\sum$ ,可以计算出从该正态分布取样得到训练集的概率。 $ L(\mu,\sum) = f_{\mu,\sum}{x_1} f_{\mu,\sum}{x_2}f_{\mu,\sum}{x_3}…f_{\mu,\sum}{x_N} $ ,这就是似然函数(Likelihood Function),其中$N$ 是训练集中某个类别样本的数量。
- $\mu^,\sum^=\arg\max_{\mu,\sum}{L(\mu,\sum)}$,当然可以求导。直觉:$\mu^=\frac{1}{N}\sum_{i=1}^{N}{x_i}$,$\sum^ = \frac{1}{N}\sum_{i=1}^{N}(x_i-\mu^*)^2T$
协方差矩阵共享 #
每个类别的特征符合一个多元正态分布,每个多元正态分布也有不同的均值和协方差矩阵。让每个类别对应的多元正态分布共享一个协方差矩阵(各个协方差矩阵的加权平均和),公式为 $\sum = \frac{N_1}{N_1+N_2}\sum_1+\frac{N_2}{N_1+N_2}\sum_2$,可以减少模型参数,缓解过拟合
极大似然估计 #
极大似然估计指已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,然后通过若干次试验,观察其结果,利用结果推出参数的大概值。一般说来,在一次试验中如果事件A发生了,则认为此时的参数值会使得 $P(A|\theta)$ 最大,极大似然估计法就是要这样估计出的参数值,使所选取的样本在被选的总体中出现的可能性为最大。
求极大似然函数估计值的一般步骤:
- 写出似然函数
- 对似然函数取对数,并整理
- 求导数
- 解似然函数
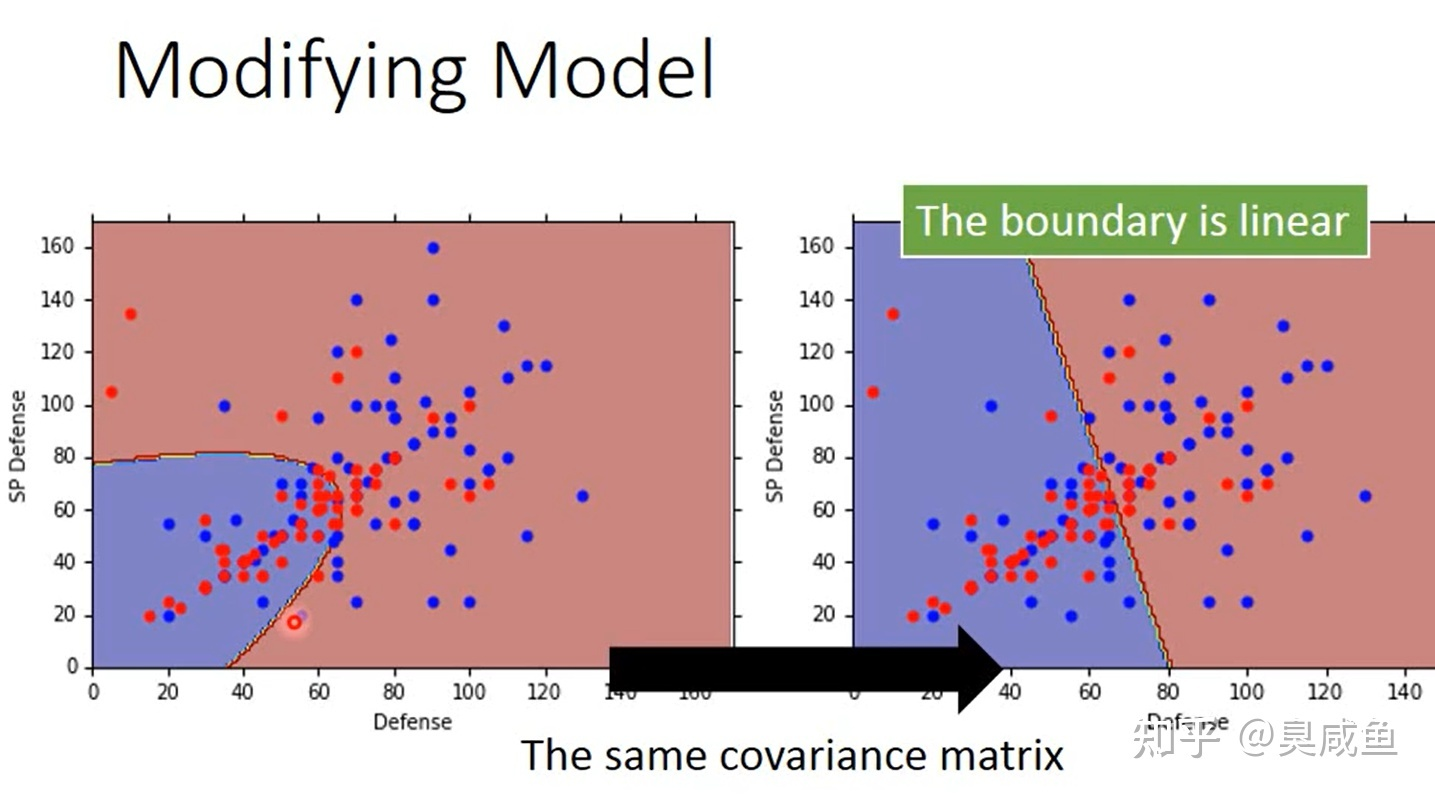
当共享协方差矩阵时,此时似然函数是$L(\mu_1,\mu_2,\sum)=f_{\mu_1,\sum}(x_1)f_{\mu_1,\sum}(x_2)…f_{\mu_1,\sum}{(x_{N1}) \times f_{\mu_2,\sum}(x_{N1+1})f_{\mu_2,\sum}(x_{N1+2})…f_{\mu_2,\sum}(x_{N1+N2})}$ ,其中 $N_1$ 为训练集中类别 $C_1$ 的样本数、$N_2$ 为训练集中类别 $C_2$ 的样本数。当只有两个类别、两个特征时,如果共享协方差矩阵,那最终得到的两个类别的分界线是直线(横纵轴是两个特征),这一点可以在下文解释。
- 除了正态分布,还可以用其它的概率模型。 比如对于二值特征,可以使用伯努利分布(Bernouli Distribution)。
- 朴素贝叶斯分类:如果假设样本各个维度的数据是互相独立的,那这就是朴素贝叶斯分类器(Naive Bayes Classfier)。
Sigmoid 函数 #
由上我们可知,$P(C_1|x)= \frac{P(x|C_1)P(C_1)}{P(x)}=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}=\frac{1} {1+\frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1)}}$ ,令 $z=\ln{\frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)}}$ ,则 $P(C_1|x) =\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}=\frac{1} {1+\frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1)}}=\frac{1}{1+e^{-z}} = \delta(z)$ ,这就是Sigmoid函数。
如果共享协方差矩阵,经过运算可以得到 $z=w_T+b$ 的形式,其中常量 $w_T = (\mu_1-\mu_2)^T\sum^{-1}$,常量 $b=-\frac{1}{2}(\mu_1)^T(\sum_1)^{-1}\mu_1+\frac{1}{2}(\mu_2)^T(\sum_2)^{-1}\mu_2+\ln{\frac{N_1}{N_2}}$ ,即形如 $P(C_1|x) = \delta(w\cdot x+b)$ 。
4.3 分类模型之逻辑回归 #
逻辑回归 #
假设训练集如下图所示,有2个类别 $C_1$ 和 $C_2$ ,下图表格中的每列为一个样本。
| $x_1$ | $x_2$ | $x_3$ | … | $x_N$ |
|---|---|---|---|---|
| $C_1$ | $C_1$ | $C_2$ | … | $C_1$ |
| $\hat{y_1} =1$ | $\hat{y_2} =1$ | $\hat{y_3} = 0$ | … | $\hat{y_n} =1$ |
例如,第一列表示样本 $x_1$ 的类别为 $C_1$ ,所以它标签是 $\hat{y_1}$ 是1。
模型定义 #
在分类(Classification)一节中,我们要找到一个模型 $P_{w,b}(C_1|x)$ ,如果 $P_{w,b}(C_1|x)\geq0.5$ ,则 $x$ 属于类别 $C_1$ ,否则属于类别 $C_2$ 。可知 $P_{w,b}(C_1|x) = \sigma(z)$ ,其中 $\sigma(z)=\frac{1}{1+e^{-z}}$ (Sigmoid Fuction),$z=w \cdot x+b=\sum^{N}{i=1}{w_ix_i+b} $ 。最终我们找到了模型 $f{w,b(x)}=\sigma(\sum^N_{i=1}{w_ix_i+b})$。 最终我们找到了模型 $f_{w,b(x)=\sigma(\sum^N_{i=1}{w_ix_i+b})}$ ,这其实就是逻辑回归(Logistic Regression)。
损失函数 #
从模型 $ f_{w,b}(x)=P_{w,b}(C_1|x) $ 中取样得到训练集的概率为: $ L(w,b)=f_{w,b}(x_1)f_{w,b}(x_2)(1-f_{w,b}(x_3))…f_{w,b}(x_N) $ (似然函数)。
我们要求出 $w^,b^=\arg\max_{w,b}L(w,b)$,等同于 $w^,b^=\arg\min_{w,b}-\ln{L(w,b)}$ (对数似然方程,Log-likelihood Equation)。
而 $ -\ln{L(w,b)=-\ln{f_{w,b}{x_1}} -\ln{f_{w,b}{x_2}}} -\ln{(1-f_{w,b}{x_3})}…$ ,其中 $ \ln{f_{w,b}(x_N)=\hat{y^N}\ln{f_{w,b}{(x^N)}} + (1-\hat{y^N})\ln{(1-f_{w,b}{(x^N)})}} $ ,所以 $ -\ln{L(w,b)=\sum^N_{n=1}{-[\hat y^N\ln{f_{w,b}(x^N)}+(1-\hat y^n)\ln(1-f_{w,b}(x^N))]}} $ ,式中N用来选择某个样本。
假设有两个伯努利分布 $p$ 和 $q$ ,在 $p$ 中有 $p(x=1)=\hat {y^N}$ ,$p(x=0)=1-\hat{y^N}$ ,在 $q$ 中有 $q(x=1)=f(x_N)$ ,$q(x=0)=1-f(x_N)$ ,则 $p$ 和 $q$ 的交叉熵(Cross Entropy,代表两个分布有多接近,两个分布一摸一样时交叉熵为0),为 $H(p,q)=-\sum_x{p(x)\ln(q(x))}$ 。所以损失函数 $L(f)=\sum^N_{n=1}{C(f(x_n),\hat{y^N})}$ ,其中 $C(f(x_N),\hat{y^N})=-[\hat y^N\ln{f_{w,b}(x^N)}+(1-\hat y^n)\ln(1-f_{w,b}(x^N))]$ ,即损失函数为所有样本的 $f(x_N)$ 与 $\hat{y_N}$ 的交叉熵之和,式中 $N$ 用来选择某个样本。
梯度 #
$ \frac{-\ln{L(w,b)}}{\sigma_{w_i}} = \sum^N_{n=1}{-(\hat{y^n}-f_{w,b}{(x^n)})x_i^n} $ ,其中 $i$ 用来选择数据的某个维度, $n$ 用来选择某个样本, $ N $ 为数据集中样本个数。该式表明,预测值与label相差越大时,参数更新的步幅越大,这符合常理。
逻辑回归 VS 线性回归 #

模型 #
逻辑函数模型比线性回归模型多了一个sigmoid函数。逻辑函数输出是[0,1],而线性回归的输出是任意值。
损失函数 #
逻辑回归模型使用的数据集中label的值必须是0或1,而线性回归模型训练集中label的值是真实值。
图中的 $\frac{1}{2}$ 是为了方便求导 。这里有一个问题,为什么逻辑回归模型中不适用Square Error呢?这个问题的答案见下文
梯度 #
逻辑回归模型和线性回归模型的梯度公式一样
为什么逻辑回归模型中不使用Square Error #

由上图可知,当label的值为1时,不管预测值是0还是1,梯度都为0,当label值为0时也是这样。
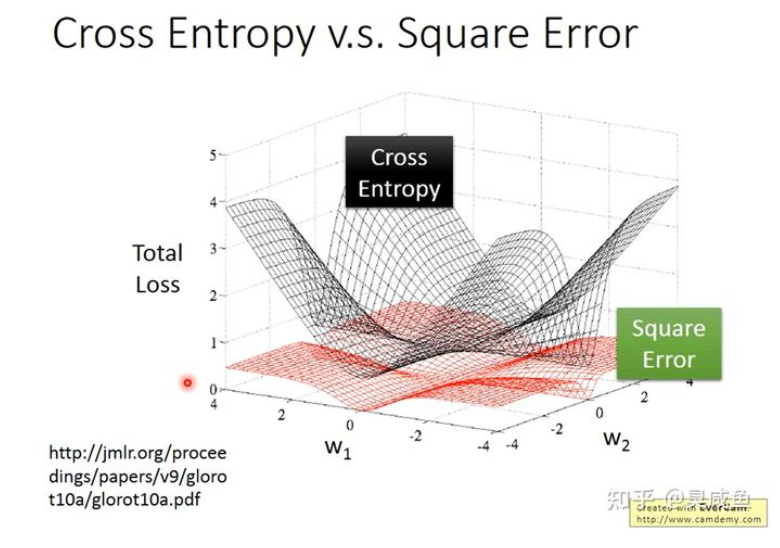
如下图所示,如果在逻辑回归中使用Square Error,当梯度接近0时,我们无法判断目前与最优解的距离,也就无法调节学习率;并且在大多数时候梯度都是接近0的,收敛速度会很慢。
判别模型 VS 生成模型 #
形式对比 #
逻辑回归是一个判别模型(Discriminative Model),用正态分布描述后验概率(Posterior Probability)则是生成模型(Generative Model)。如果生成模型中公用协方差矩阵,那两个模型/函数集其实是一样的,都是 $ P(C_1|x)=\sigma(w \cdot x+b) $ 。因为做了不同的假,即使是使用同一个数据集、同一个模型,找到的函数是不一样的。
优劣对比 #
- 如果现在数据很少,当假设了概率分布以后,就可以需要更少的数据用于训练,受数据影响较小;而判别模型就只根据数据来学习,易受数据影响,需要更多数据
- 当假设了概率分布后,生成模型受数据影响小,对噪声的鲁棒性更强
- 对于生成模型来讲,先验的和基于类别的概率(Prors and class-dependent probabilities),即 $ P(C_1) $ 和 $ P(C_2) $ ,可以从不同的来源估计得到。以语音识别为例,如果用生成模型,可能并不需要声音的数据,网上的文本也可以用来估计某段文本出现的概率
多分类(Multi-class Classification) #
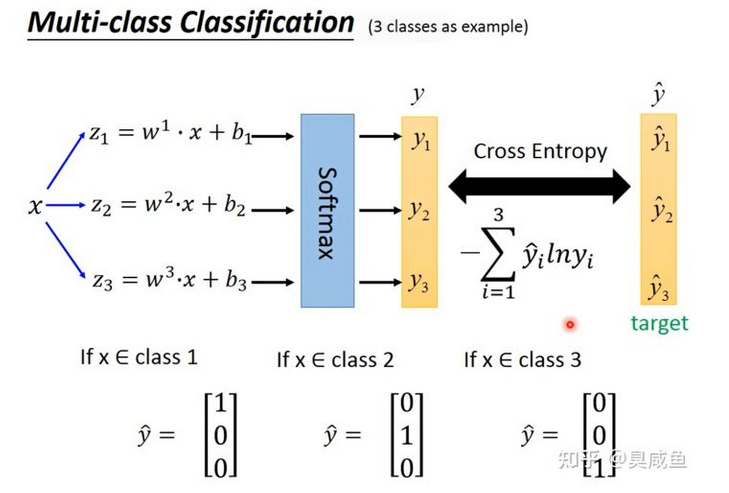
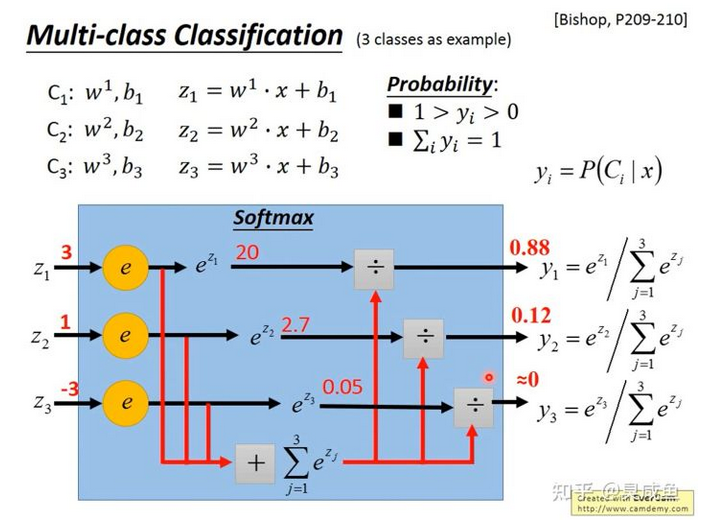
以3个类别 $C_1、C2和 C3$ 为例,分别对应参数$w_1、b_1、W_2、b_2、W_3、b_3$,即$z_1=w_1 \cdot x+b_1、z_2=w_2 \cdot x+b_2、z_3=w_3 \cdot x+b_3$
Softmax #
使用softmax($y_i=\frac{e_{z_i}}{\sum^c_{j=1}{e_{z_j}}}$)
softmax公式中为什么要用$e$?这是由原因的/可解释的,可以看下PRML,也可以搜一下最大熵
最大熵(Maximum Entropy)其实也是一种分类器,和逻辑回归一样,只是从信息论的角度来看
损失函数 #
计算预测值$y$和$\hat y$都是一个向量,即$-\sum^3_{i=1}{{\hat y}_i\ln{y_i}}$
这时需要使用one-hot编码:如果$x\in C_1$,则$y=\begin{bmatrix} 1\ 0\ 0\ \end{bmatrix}$;如果$x\in C_1$,则$y=\begin{bmatrix} 0\ 1\ 0\ \end{bmatrix}$;如果$x\in C_1$,则$y=\begin{bmatrix} 0\ 0\ 1\ \end{bmatrix}$。
梯度 #
和逻辑回归的思路一样。
逻辑回归的局限性 #
如下图所示,假如有2个类别,数据集中有4个样本,每个样本有2维特征,将这4个样本画在图上。
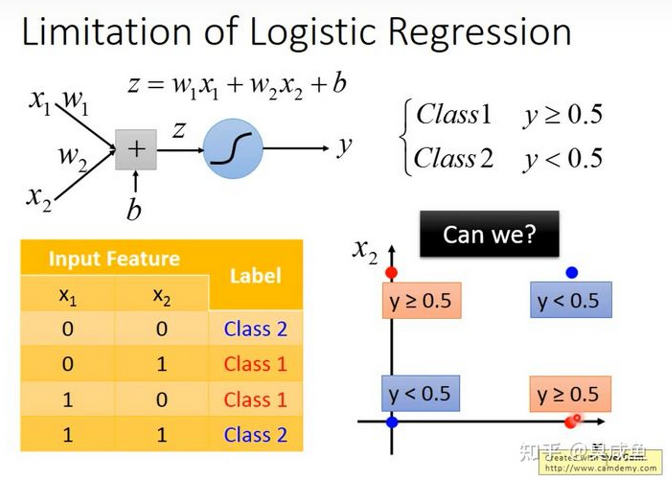
如下图所示,假如用逻辑回归做分类,即$y=\sigma(z)=\sigma(w_1\cdot x_1+w_2\cdot x_2+b)$,我们找不到一个可以把“蓝色”样本和“红色”样本间隔开的函数。
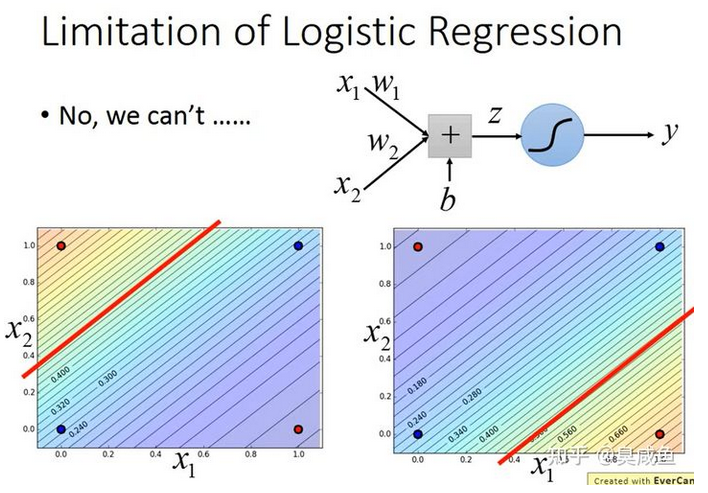
假如一定要用逻辑回归,那我们可以怎么办呢?我们可以尝试特征变换(Feature Transformation)。
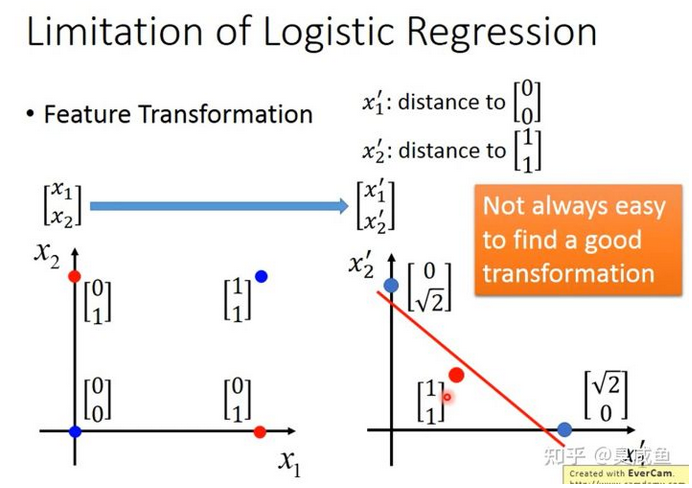
特征变换(Feature Transformation) #
在上面的例子中,我们并不能找到一个能将蓝色样本和红色样本间隔开的函数。如下图所示,我们可以把原始的数据/特征转换到另外一个空间,在这个新的特征空间中,找到一个函数将“蓝色”样本和“红色”样本间隔开。比如把原始的两维特征变换为$\begin{bmatrix} 0\ 0\ \end{bmatrix} 和 \begin{bmatrix} 1\ 1\ \end{bmatrix}$ 的距离,在这个新的特征空间,“蓝色”样本和“红色”样本是可分的。
但有一个问题是,我们并不一定知道怎么进行特征变换。或者说我们想让机器自己学会特征变换,这可以通过级联逻辑回归模型实现,即把多个逻辑回归模型连接起来,如下图所示。下图中有3个逻辑回归模型,根据颜色称它们为小蓝、小绿和小红。小蓝和小绿的作用是分别将原始的2维特征变换为新的特征$x_1’和x_2’$,小红的作用是在新的特征空间$\begin{bmatrix} x_1’\ x_2’\ \end{bmatrix}$上将样本分类。
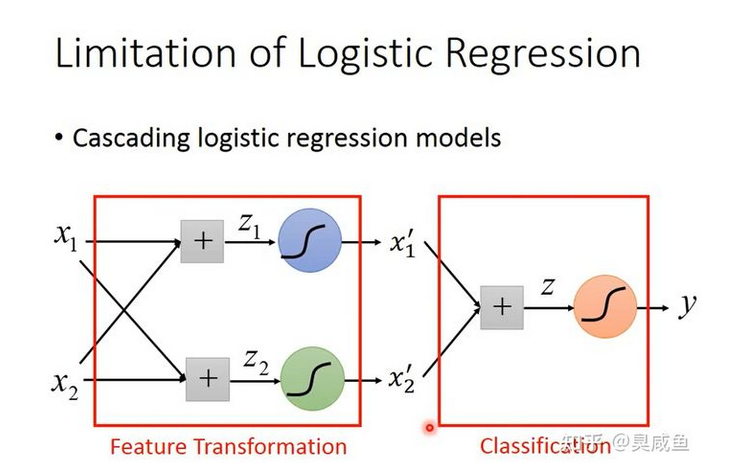
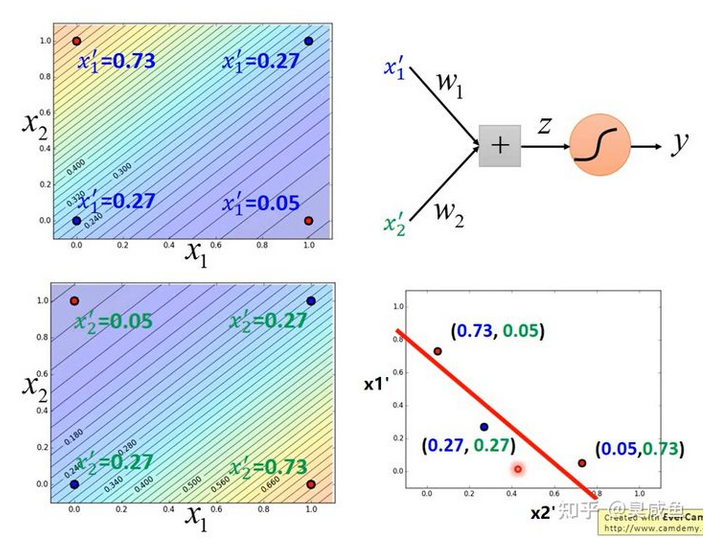
如下图所示,举一个例子。小蓝的功能是(下图左上角),离$(1,0)$越远、离$(0,1)$越近,则$x_1’$越大;小蓝的功能是(下图左上角),离$(1,0)$越远、离$(0,1)$越近,则$x_1’$越小。小蓝和小绿将特征映射到新的特征空间$\begin{bmatrix} x_1’\ x_2’\ \end{bmatrix}$中,结果见下图右下角,然后小红就能找到一个函数将“蓝色”样本和“红色”样本间隔开。
神经网络(Neural Network) #
假如把上例中的一个逻辑回归叫做神经元(Neuron),那我们就形成了一个神经网络。
ROC #
在信号检测理论中,接收者操作特征曲线(receiver operating characteristic curve,或者叫ROC曲线)是 坐标图式的分析工具,用于 (1) 选择最佳的 信号侦测模型、舍弃次佳的模型。 (2) 在同一模型中设定最佳阈值。在做决策时,ROC分析能不受成本/效益的影响,给出客观中立的建议。
ROC曲线首先是由二战中的电子工程师和雷达工程师发明的,用来侦测战场上的敌军载具(飞机、船舰),也就是信号检测理论。之后很快就被引入了心理学来进行信号的知觉检测。数十年来,ROC分析被用于医学、无线电、生物学、 犯罪心理学领域中,而且最近在机器学习(machine learning)和数据挖掘(data mining)领域也得到了很好的发展。
术语
- 阳性(P, positive)
- 阴性(N, Negative)
- 真阳性 (TP, true positive) 正确的肯定。又称:命中 (hit)
- 真阴性 (TN, true negative) 正确的否定。又称:正确拒绝 (correct rejection)
- 伪阳性 (FP, false positive) 错误的肯定,又称:假警报 (false alarm),第一型错误伪阴性 (FN, false negative) 错误的否定,又称:未命中 (miss),第二型错误
- 真阳性率 (TPR, true positive rate) 又称:命中率 (hit rate)、 敏感度(sensitivity) TPR = TP / P = TP / (TP+FN)
- 伪阳性率(FPR, false positive rate) 又称:错误命中率,假警报率 (false alarm rate) FPR = FP / N = FP / (FP + TN)
- 准确度 (ACC, accuracy) ACC = (TP + TN) / (P + N) 即:(真阳性+真阴性) / 总样本数真阴性率 (TNR) 又称:特异度 (SPC, specificity) SPC = TN / N = TN / (FP + TN) = 1 - FPR
- 阳性预测值 (PPV) PPV = TP / (TP + FP)
- 阴性预测值 (NPV) NPV = TN / (TN + FN)
- 假发现率 (FDR) FDR = FP / (FP + TP)