6.1 神经网络训练问题与解决方案 #
明确问题类型及其对应方法 #
在深度学习中,一般有两种问题:
- 在训练集上性能不好
- 在测试集上性能不好。
当一个方法被提出时,它往往是针对这两个问题其中之一的,比如dropout方法是用来处理在测试集上性能不好的情况。
处理神经网络在训练集上性能不好的情况和方法 #
- 修改神经网络架构,比如换成更好的激活函数: sigmoid函数会导致梯度消失,可以换成ReLU、Leaky ReLU、Parametric ReLU、Maxout
- 调整学习率: 比如RMSProp、Momentum、Adam
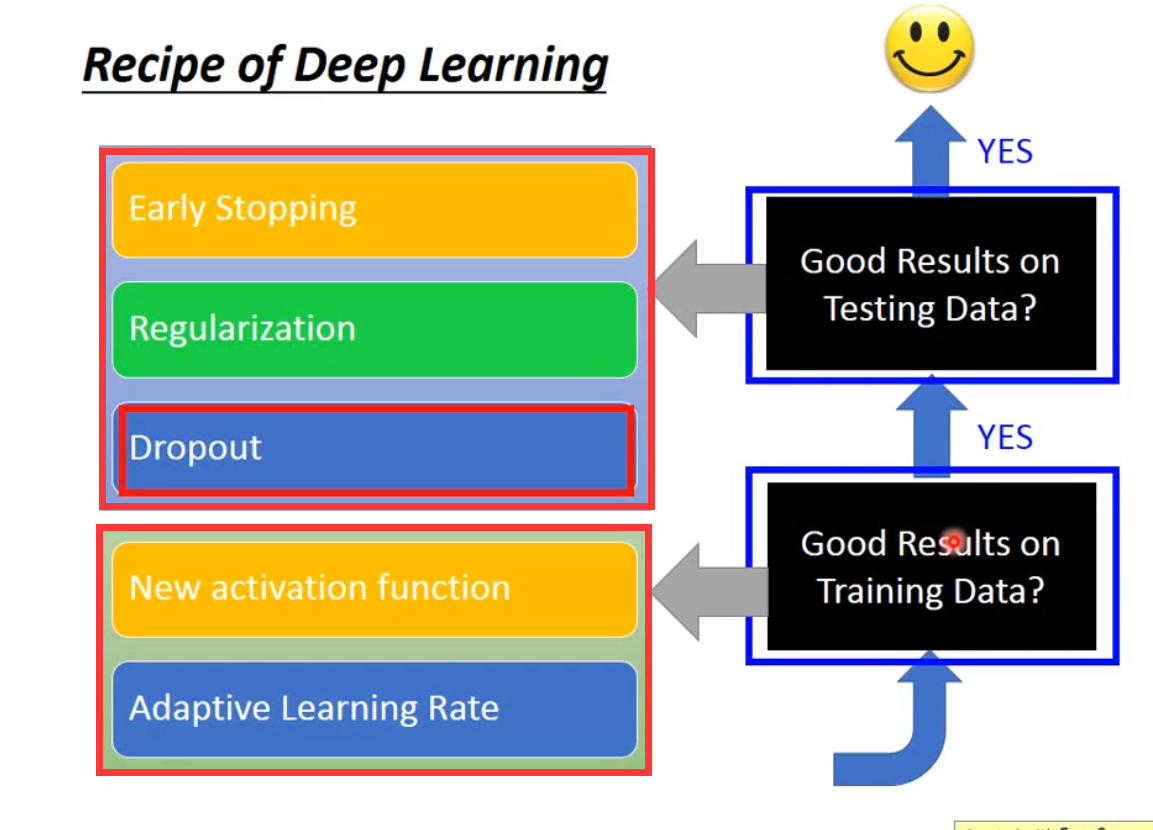
处理神经网络在测试集上性能不好的情况和方法 #
- Early Stopping、Regularization,这两个是比较传统的方法,不只适用于深度学习
- Dropout,比较有深度学习的特色
一些性能优化方法的简介 #
下面3点都是在增加模型的随机性,鼓励模型做更多的exploration。
- Shuffling: 输入数据的顺序不要固定,mini-batch每次要重新生成
- Dropout: 鼓励每个神经元都学到东西,也可以广义地理解为增加随机性
- Gradient noise: 2015年提出,计算完梯度后,加上Gaussian noise。 随着迭代次数增加,noise应该逐渐变小。
下面3点是关于学习率调整的技巧
- warm up: 开始时学习率较小,等稳定之后学习率变大
- Curriculum learning: 2009年提出,先使用简单的数据训练模型(一方面此时模型比较弱,另一方面在clean data中更容易提取到核心特征),然后再用难的数据训练模型。 这样可以提高模型的鲁棒性。
- Fine-tuning
下面3点是关于数据预处理的技巧,避免模型学习到太极端的参数
- Normalization: 有Batch Normalization、Instance Normalization、Group Normalization、Layer Normalization、Positional Normalization
- Regularization
6.2 神经网络精度低不一定是因为过拟合 #
- 相比于决策树等方法,神经网络更不容易过拟合:K近邻、决策树等方法在训练集上更容易得到100%等很高的正确率,神经网络一般不能,训练神经网络首先遇到的问题一般是在训练集上的精度不高。
- 不要总是把精度低归咎于过拟合:如果模型在训练集上精度高,对于K近邻、决策树等方法我们可以直接判断为过拟合,但对于神经网络来说我们还需要检查神经网络在测试集上的精度。如果神经网络在训练集上精度高但在测试集上精度低,这才说明神经网络过拟合了。 如果56层的神经网络和20层的神经网络相比,56层网络在测试集上的精度低于20层网络,这还不能判断为56层网络包含了过多参数导致过拟合。一般来讲,56层网络优于20层网络,但如果我们发现56层网络在训练集上的精度本来就低于20层网络,那原因可能有很多而非过拟合,比如56层网络没训练好导致一个不好的局部最优、虽然56层网络的参数多但结构有问题等等。
- 感兴趣可以看看ResNet论文** Deep Residual Learning for Image Recognition**,这篇论文可能与该问题有关。
6.3 常用激活函数(训练集) #
梯度消失(Vanishing Gradient Problem) #
定义:1980年代常用的激活函数是sigmoid函数。以MNIST手写数字识别为例,在使用sigmoid函数时会发现随着神经网络层数增加,识别准确率逐渐下降,这个现象的原因并不是过拟合(原因见上文),而是梯度消失。
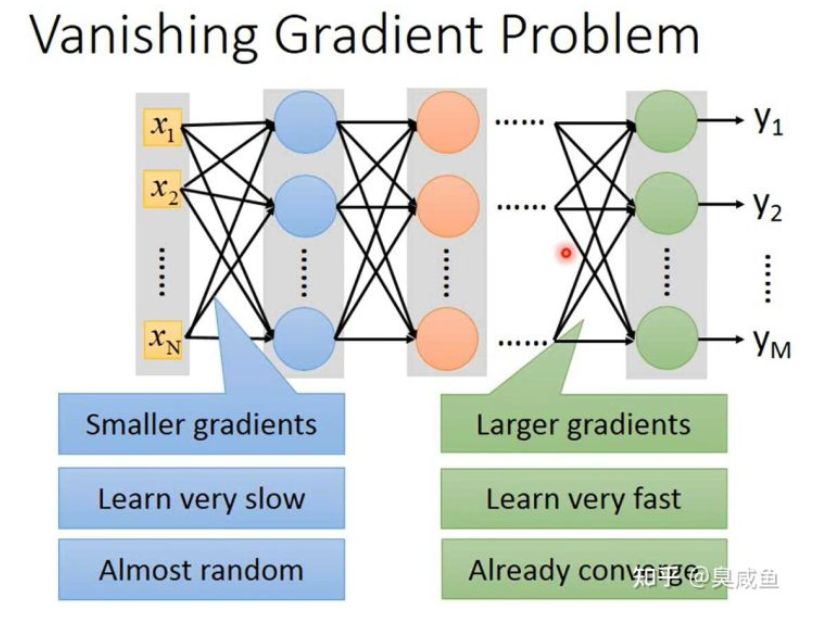
如上图所示,当神经网络层数很多时,靠近输入层的参数的梯度会很小,靠近输出层的参数的梯度会很大。当每个参数的学习率相同时,靠近输入层的参数会更新得很慢,靠近输出层的几层参数会更新得很快。所以,当靠近输入层的参数几乎还是随机数时,靠近输出层的参数已经收敛了。
- 原因: 按照反向传播的式子,这确实是会发生的。直观感觉上,sigmoid函数输入的范围是无穷大,但输出的范围是[0,1],也就是说sigmoid函数减弱了输入变化导致输出变化的幅度。那为什么靠近输出层的参数的梯度更大呢?sigmoid函数是一层层叠起来的,不断地减弱靠近输入层的参数的变化导致输出变化的幅度,所以更靠后的参数的梯度越大。
- 解决方法: Hinton提出无监督逐层训练方法以解决这个问题,其基本思想是每次训练一层隐节点。 后来Hinton等人提出修改激活函数,比如换成ReLU。
ReLU(Rectified Linear Unit) #
定义: 当输入小于等于0时,输出为0;当输入大于0时,输出等于输入,如下图所示。
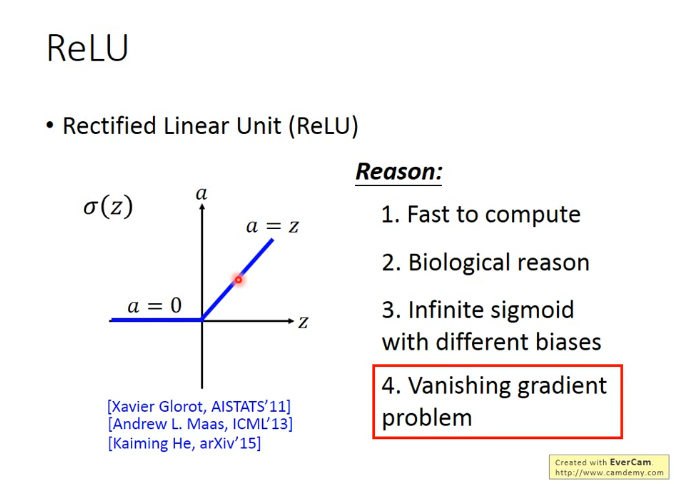
优点: 相比于sigmoid函数,它有以下优点
- 运算更快
- 更符合生物学
- 等同于无穷多个bias不同的sigmoid函数叠加起来
- 可以解决梯度消失问题
- 如何解决梯度消失问题? 当ReLU输出为0时该激活函数对神经网络不起作用,所以在神经网络中生效的激活函数都是输出等于输入,所以就不会出现sigmoid函数导致的减弱输入变化导致输出变化的幅度的情况。
- ReLU会使整个神经网络变成线性的吗? 可知有效的激活函数都是线性的,但整个神经网络还是非线性的。当输入改变很小、不改变每个激活函数的Operation Region(操作区域,大概意思就是输入范围)时,整个神经网络是线性的;当输入改变很大、改变了Operation Region时,整个神经网络就是非线性的。==目前我是凭直觉理解这一点,还未细究==
- ReLU可以做微分吗? 不用处理输入为0的情况,当输入小于0时,微分就是0,当输入大于0时微分就是1。
Leaky ReLU #
当输入小于等于0时,输出为输入的0.01倍;当输入大于0时,输出等于输入。
Parametric ReLU #
当输入小于等于0时,输出为输入的 $\alpha$ 倍;当输入大于0时,输出等于输入。
其中 $\alpha$ 是通过梯度下降学习到的参数
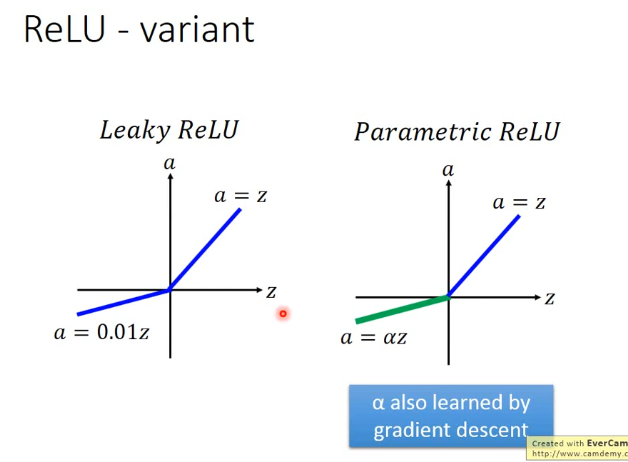
Maxout #
通过学习得到一个激活函数,人为将每层输出的多个值分组,然后输出每组值中的最大值。(跟maxpooling一模一样),其实ReLU是Maxout的一个特例。
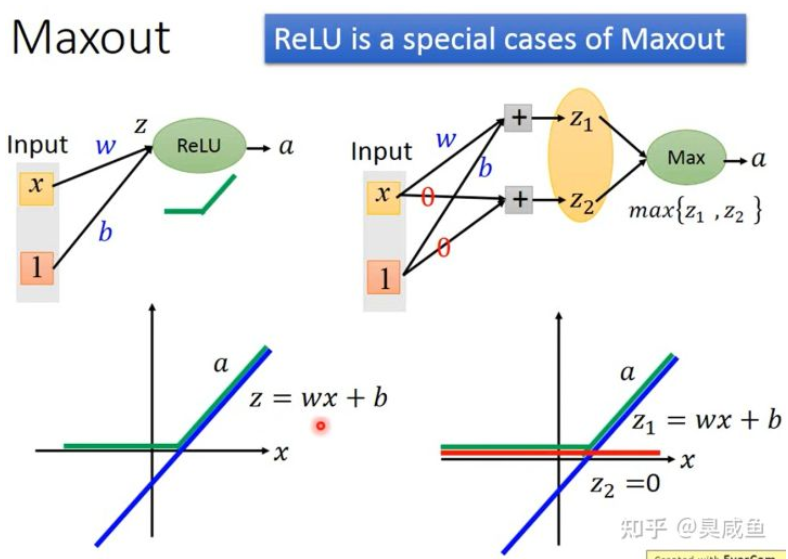
Maxout比ReLU包含了更多的函数
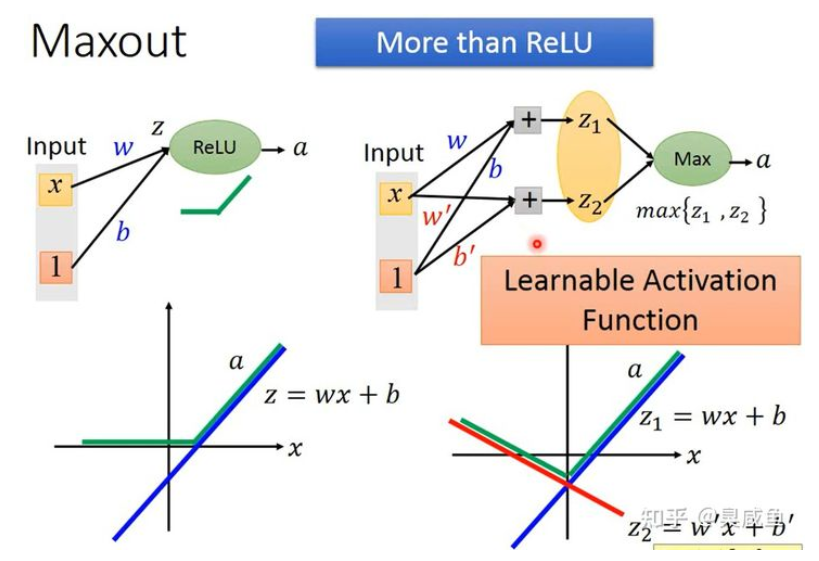
Maxout 可以得到任意的分段线性凸函数(piecewise linear convex),有几个分段取决于每组里有几个值
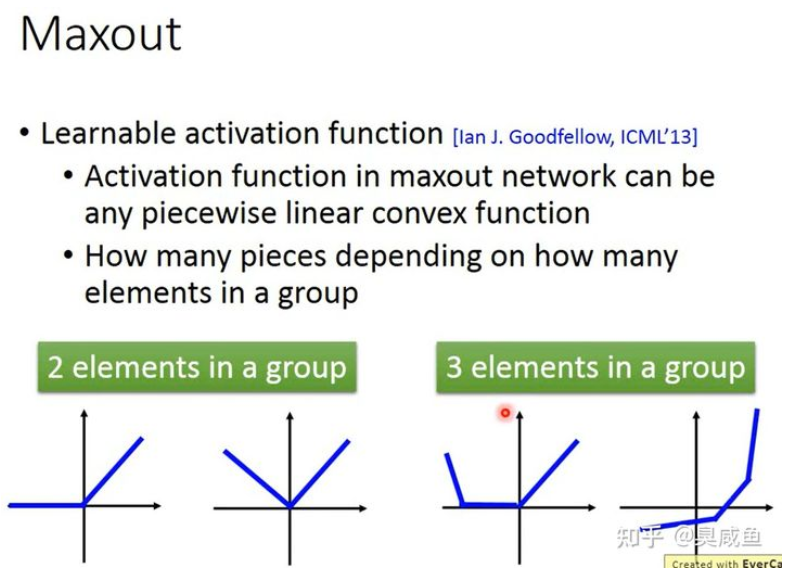
如何训练Maxout #
Maxout只是选择输出哪一个线性函数的值而已,因此Maxout激活函数还是线性的。 因为在多个值中只选择最大值进行输出,所以会形成一个比较瘦长/窄深的神经网络。 在多个值中只选择最大值进行输出,这并不会导致一些参数无法被训练:因为输入不同导致一组值中的最大值不同,所以各个参数都可能被训练到。 当输入不同时,形成的也是不同结构的神经网络。
6.4 学习率调整方法(训练集) #
Adagrad #
Adaptive Gradient Descent,自适应梯度下降,解决不同参数应该使用不同的更新速率的问题。Adagrad自适应地为各个参数分配不同学习率的算法。2011年提出,核心是每个参数(parameter)有不同的学习率。每次迭代中,学习率要除以它对应参数的之前梯度的均方根(RMS),即 $w_{t+1} = w_t-\frac{\eta}{\sqrt{\sum_{i=0}^{t}{(g_t)^2}}}g_t$ 。
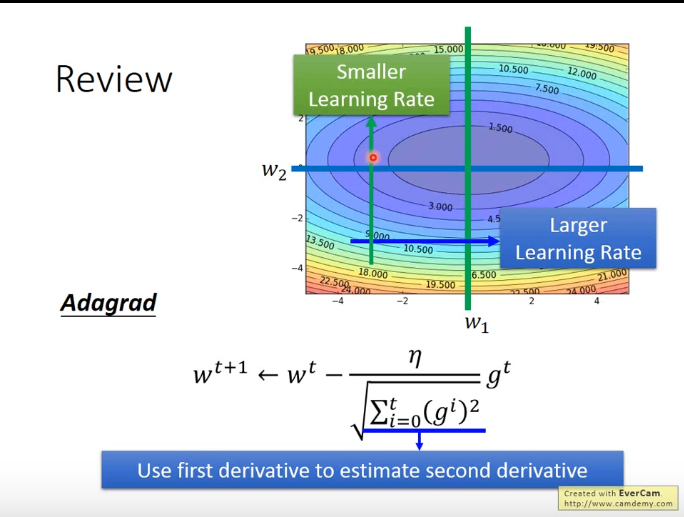
RMSProp #
背景 #
RMSProp是Adagrad的升级版,在2013年Hinton在Coursera提出。 在训练神经网络时,损失函数不一定是凸函数(局部最小值即为全局最小值),可能是各种各样的函数,有时需要较大的学习率,有时需要较小的学习率,而Adagrad并不能实现这种效果,因此产生了RMSProp。
定义 #
$w_{t+1}=w_{t}-\frac{\eta}{\sigma_t}g_t$ ($\sigma_0=g_0 , \sigma_t=\sqrt{\alpha(\sigma_{t+1})^2+(1-\alpha)(g_t)^2}$),其中 $w$ 是某个参数, $\eta$ 是学习率,$g$ 是梯度, $\alpha$ 代表旧的梯度的重要性,值越小则旧的梯度越不重要。
神经网络中很难找到最优的参数吗? #
面临的问题有plateau、saddle point和local minima。

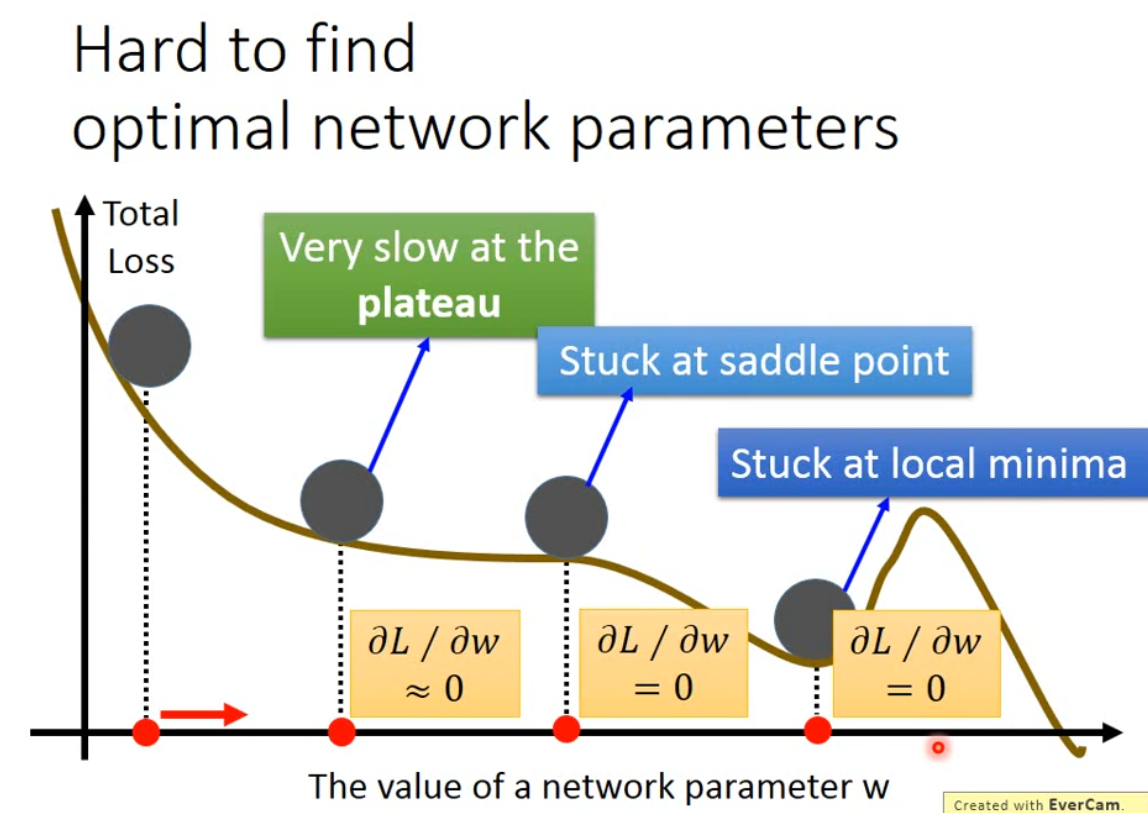
2007年有人(名字读音好像是young la ken)指出神经网络的error surface是很平滑的,没有很多局部最优。假设有1000个参数,一个参数处于局部最优的概率是 $p$ ,则整个神经网络处于局部最优的概率是 $p^{1000}$ ,这个值是很小的。
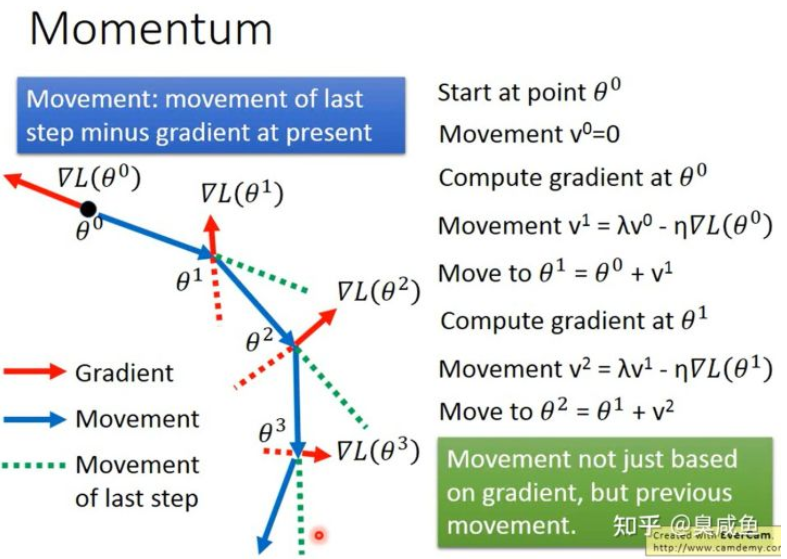
Momentum #
如何处理停滞期、鞍点、局部最小值等问题? #
考虑现实世界中物体具有惯性、动量(Momentum)的特点,尽可能避免“小球”陷入error surface上的这几种位置。
定义 #
1986年提出。如下图所示,不仅考虑当前的梯度,还考虑上一次的移动方向:$v_t = \lambda v_{t-1}-\eta g_t$ , $v_0=0$,其中 $t$ 是迭代次数,$v$ 指移动方向(movement),类似物理里的速度,$g$ 是梯度(gradient),$\lambda$ 用来控制惯性的重要性,值越大代表惯性越重要,$\eta$ 是学习率
Adam #
RMSProp+Momentum+Bias Correction,2015年提出
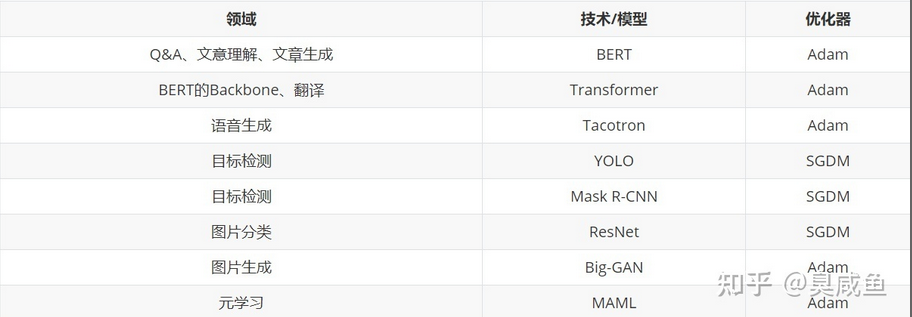
Adam VS SGDM #
目前常用的就是Adam和SGDM。
- Adam训练速度快,large generalization gap(在训练集和验证集上的性能差异大),但不稳定;
- SGDM更稳定,little generalization gap,更加converge(收敛)。
- SGDM适用于计算机视觉,Adam适用于NLP、Speech Synthesis、GAN、Reinforcement Learning。
#### SWATS
2017年提出,尝试把Adam和SGDM结合,其实就是前一段时间用Adam,后一段时间用SGDM,但在切换时需要解决一些问题。
尝试改进Adam #
- AMSGrad
- Adam的问题: Non-informative gradients contribute more than informative gradients. 在Adam中,之前所有的梯度都会对第 $t$ 步的movement产生影响。然而较早阶段(比如第1、2步)的梯度信息是相对无效的,较晚阶段(比如 $t-1$ 、$t-2$ 步)的梯度信息是相对有效的。在Adam中,可能发生较早阶段梯度相对于较晚阶段梯度比重更大的问题。
- 提出AMSGrad: 2018年提出
- AdaBound 2019年提出,目的也是改进Adam。
- Adam需要warm up吗?需要。 warm up:开始时学习率小,后面学习率大。 因为实验结果说明在刚开始的几次(大概是10次)迭代中,参数值的分布比较散乱(distort),因此梯度值就比较散乱,导致梯度下降不稳定。
- RAdam 2020年提出
- Lookahead 2019年提出,像一个wrapper一样套在优化器外面,适用于Adam、SGDM等任何优化器。 迭代几次后会回头检查一下。
- Nadam 2016年提出,把NAG的概念应用到Adam上。
- AdamW 2017年提出,这个优化器还是有重要应用的(训练出了某个BERT模型)。
尝试改进SGDM #
- LR range test 2017年提出
- Cyclical LR 2017年提出
- SGDR 2017年提出,模拟Cosine但并不是Cosine
- One-cycle LR 2017年提出,warm-up+annealing+fine-tuning
- SGDW 2017年提出
改进Momentum #
背景 #
如果梯度指出要停下来,但动量说要继续走,这样可能导致坏的结果。
- NAG(Nesterov accelerated gradient) 1983年提出,会预测下一步。
6.5 处理测试集性能不好的方法 #
6.5.1 Early Stopping #
如果学习率调整得较好,随着迭代次数增加,神经网络在训练集上的loss会越来越小,但因为验证集(Validation set)和训练集不完全一样,所以神经网络在验证集上的loss可能不降反升,所以我们应该在神经网络在验证集上loss最小时停止训练。

6.5.2 Regularization #
正则化,L2 regularization如下图所示($||\theta||^2$ ,L2范式的平方),一般不考虑bias项。

L2 regularization 的偏微分,每次都会使 $w_t$ 接近0,因为 $1-\eta\lambda$ 接近1但是小于1,比如0.99,每次成0.99,都会向0接近。

当然,regularization 也可以有其他形式,比如是 $w_i$ 绝对值的集合,成为L1 regularization,具体如下图。但是,这个方法每次使得梯度减少的速度都一样,都是 1 或 -1 乘上 $\eta\lambda$ 。

6.5.3 Dropout #
dropout是指在 深度学习网络的训练过程中,对于神经网络单元,按照一定的概率将其暂时从网络中丢弃。注意是暂时,对于随机梯度下降来说,由于是随机丢弃,故而每一个mini-batch都在训练不同的网络。
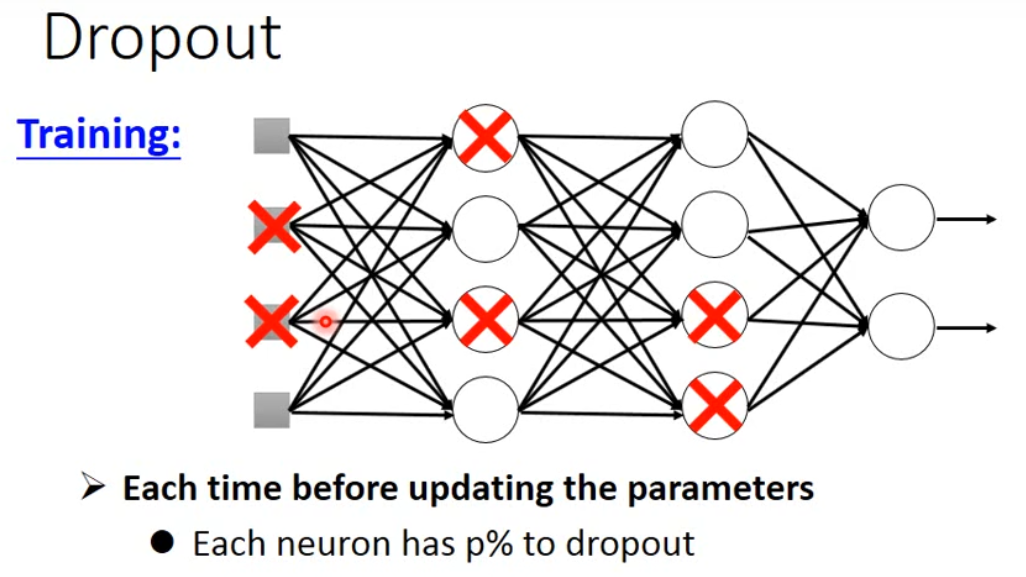
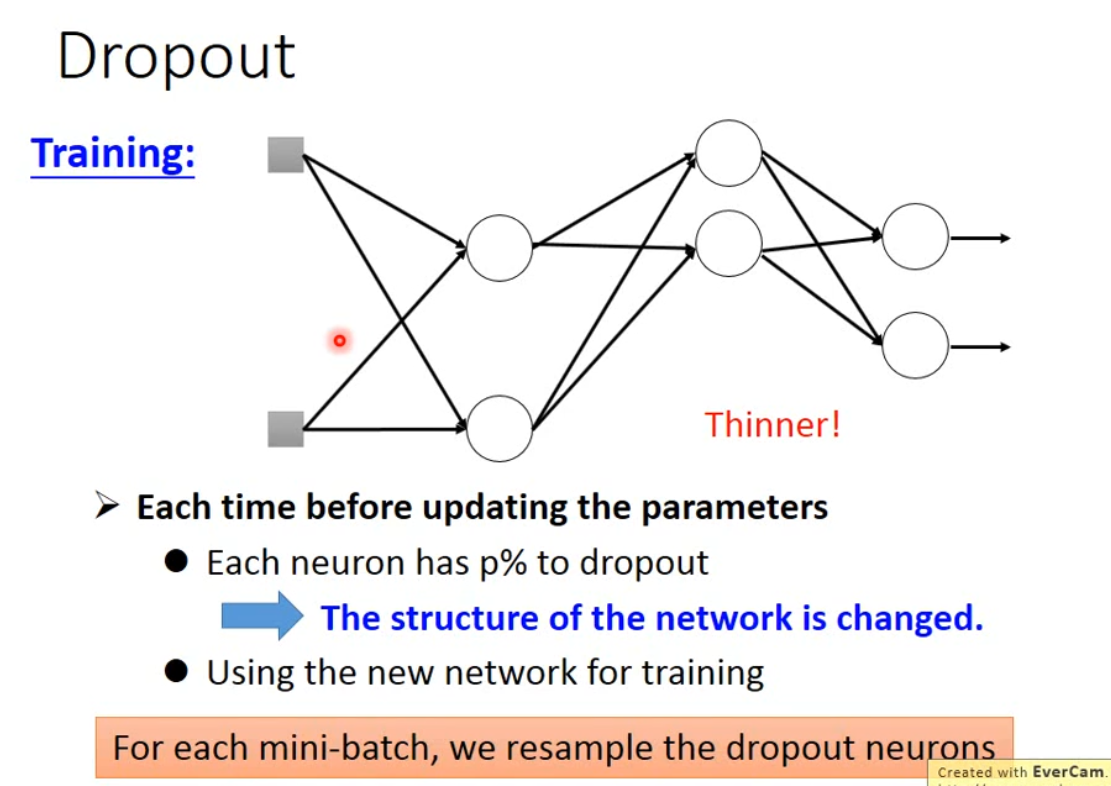
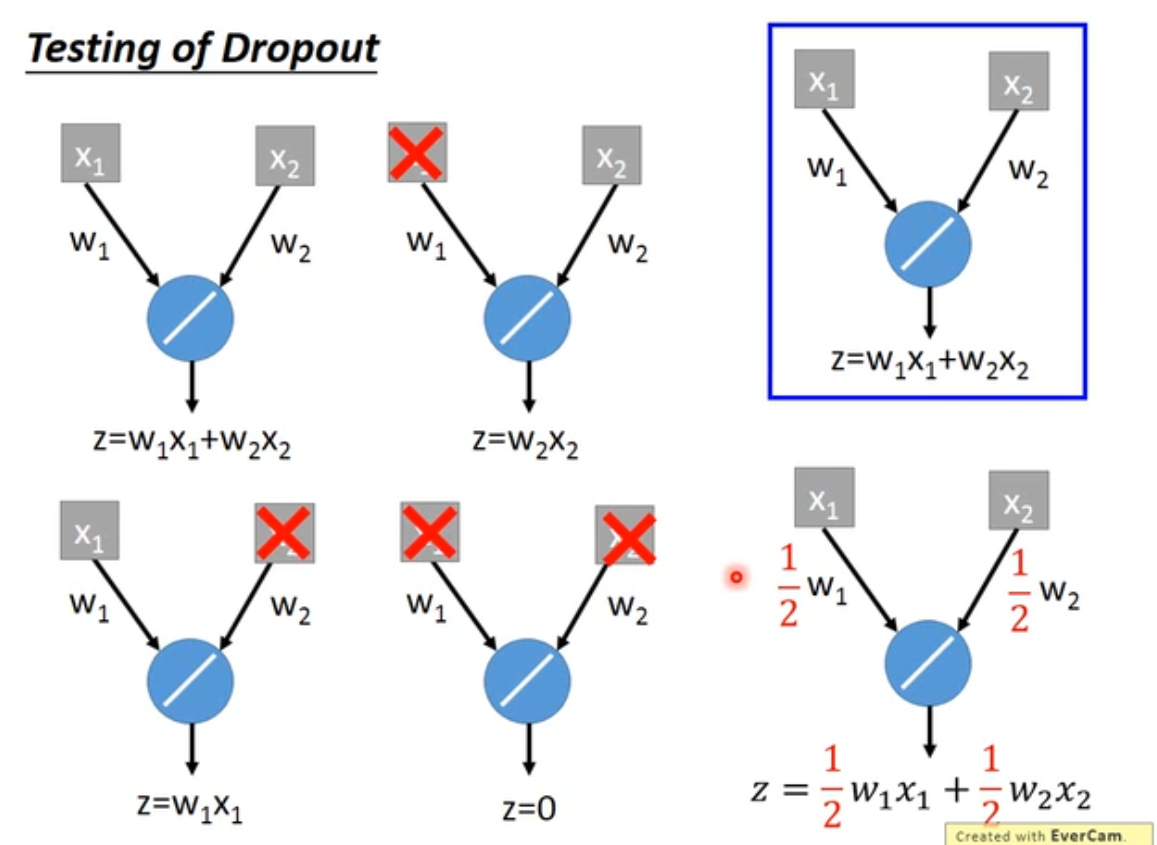
dropout 在test集合上不使用,只用在Validation set上,并且在test集合上的时候,需要把weight 乘上 $(1-p)%$ 。
直观的解释:一个团队中,每个人都希望自己的同伴会做这个工作,最后什么都没有做;但是如果你知道你的同伴会dropdout,你就会做的更好,去carry他;不过当testing的时候,没有人会去dropout,所以最后的结果会更好。
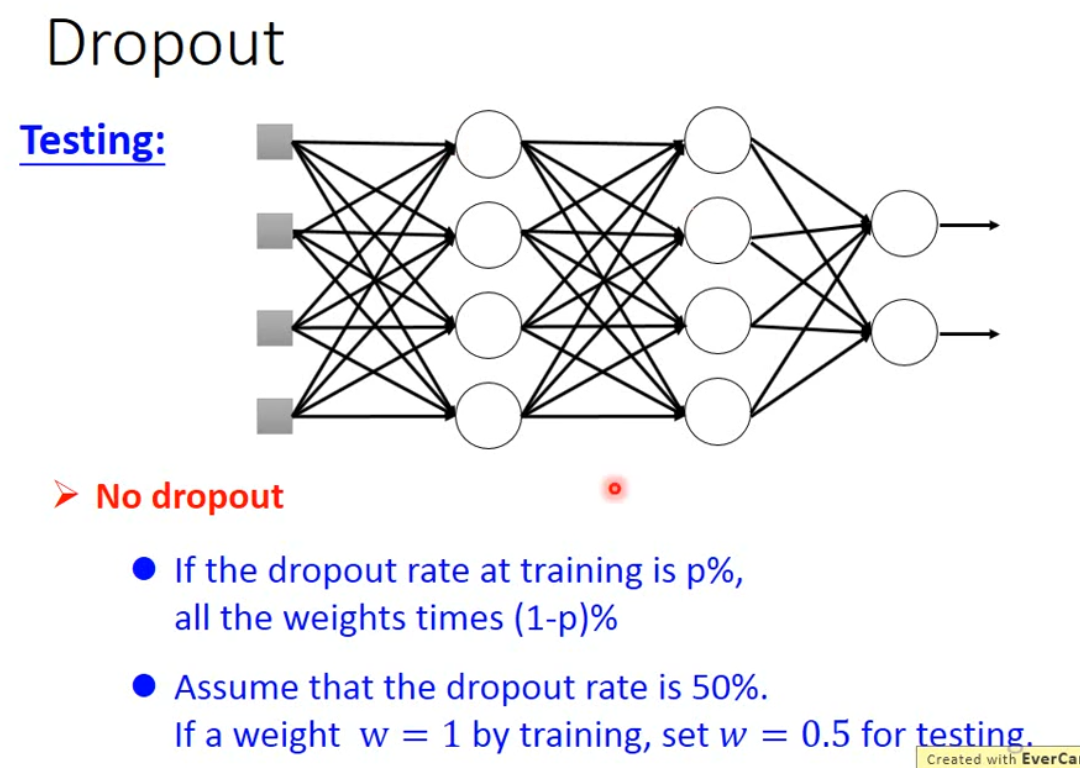
为什么要乘 $(1-p)%$ ?直观的解释如下图。

dropout是一个整体
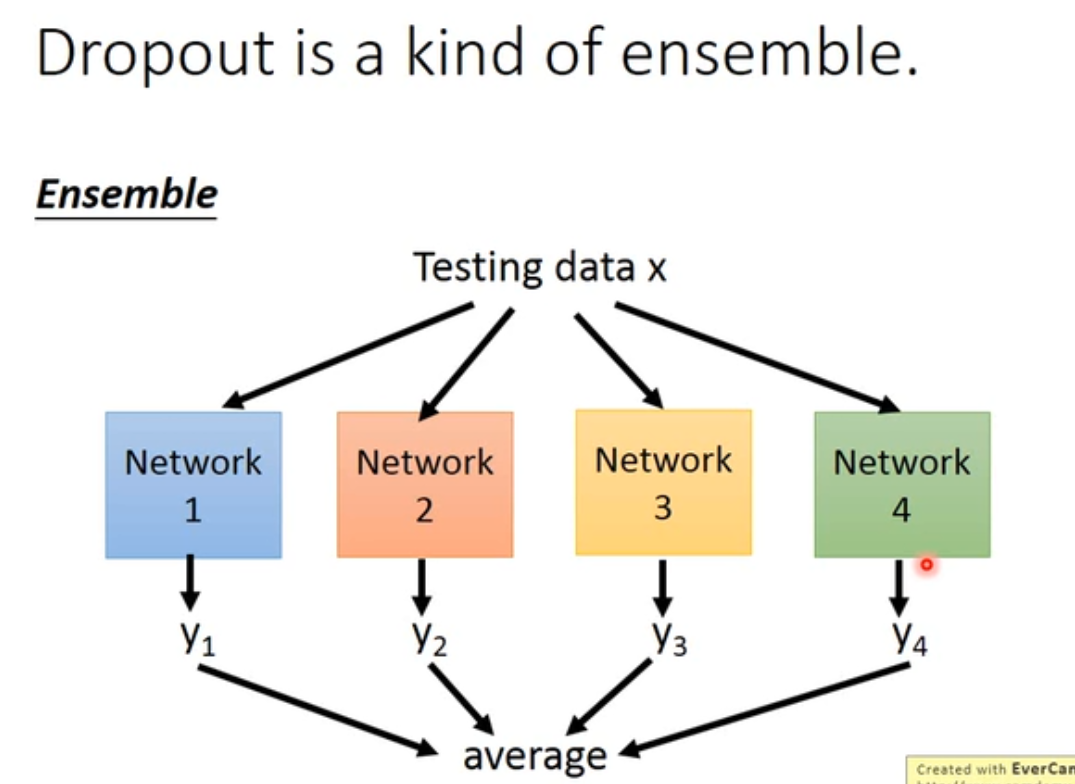
做dropout 的时候是训练了一堆 neural structual
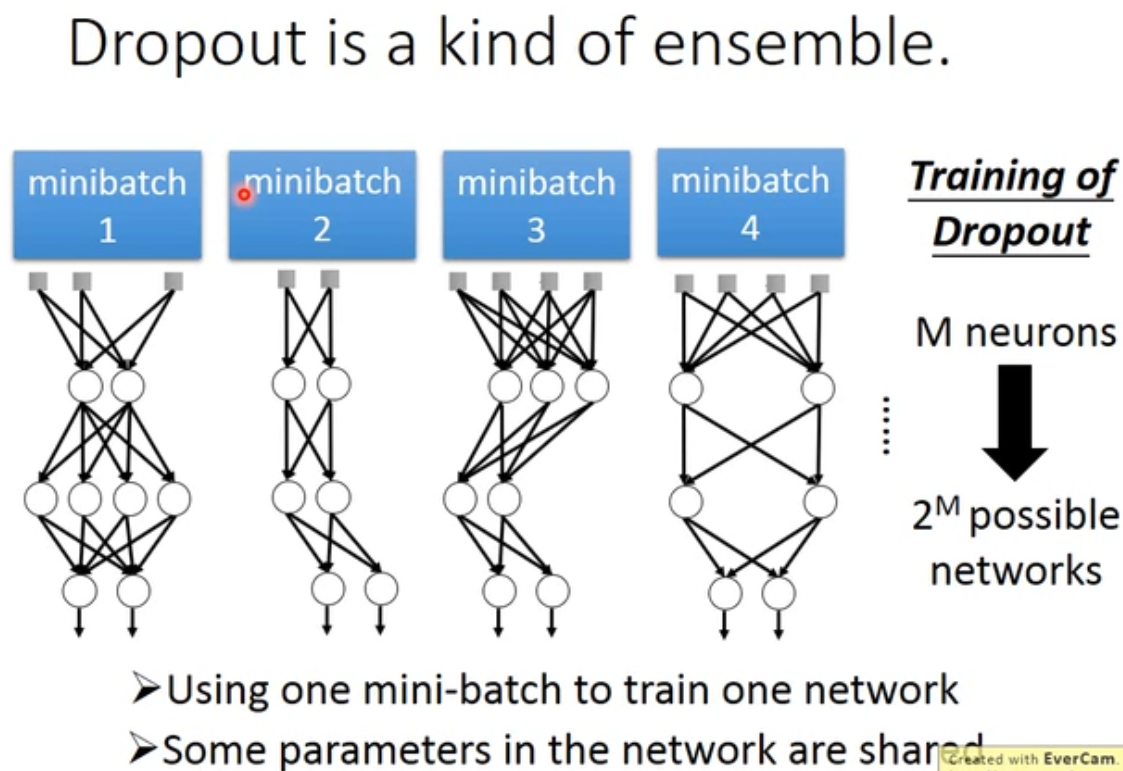
那这些值的 average 与一开始算的 $\hat y$ 是否相等呢?
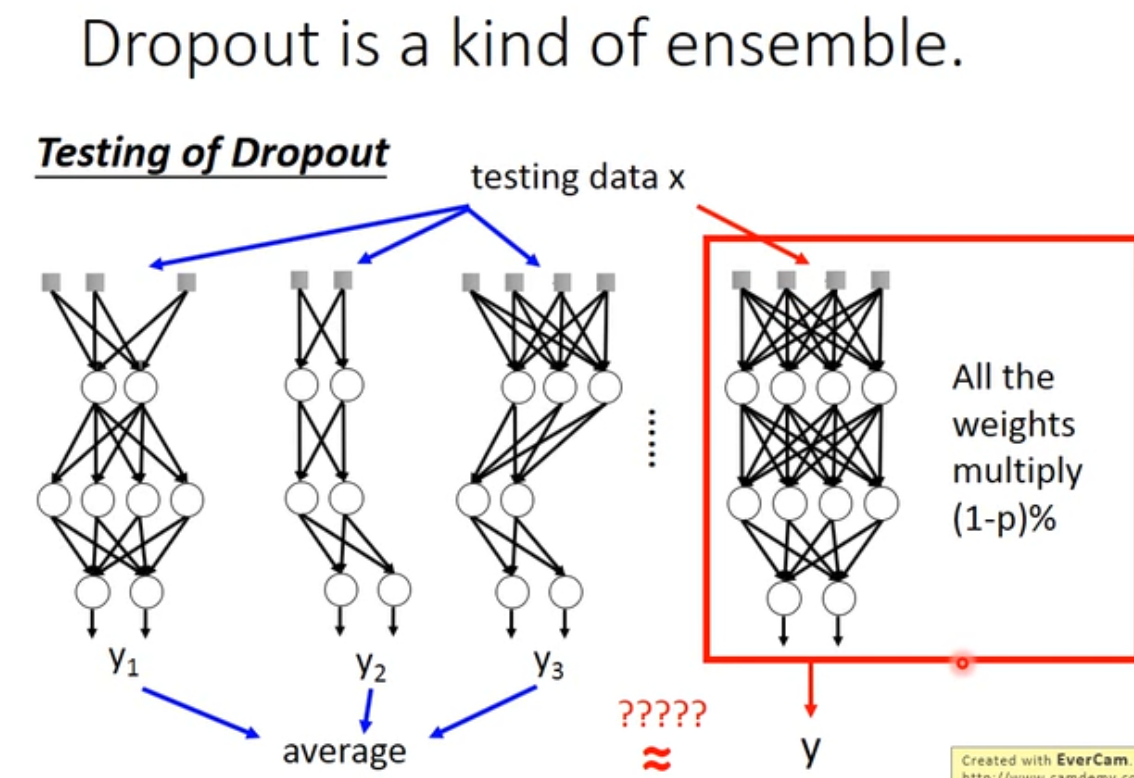
其实是一样的。