5.1引言 #
深度学习的历史 #
- 1958年:心理学家Rosenblatt提出感知机(Perceptron) 它是一个线性模型。
- 1969年:有人说感知机是线性模型,具有局限性。
- 1980年代:多层感知机(Multi-layer Perceptron) 和当今的神经网络是没有本质差别的。
- 1986年:Hinton提出反向传播算法(Backpropagation) 但是超过3个隐藏层的神经网络,还是训练不出好的结果。
- 1989年:有人提出一个隐藏层就可以得到任何函数,为什么要多层? 多层感知机慢慢淡出大家的视野。
- 2006年:受限玻尔兹曼机初始化(RBM Initialization) Hinton提出用受限玻尔兹曼机做初始化,很多人觉得这是个大突破,但实际上用处并不大。 至少让多层感知机回到大家的视野。
- 2009年:GPU
- 2011年:神经网络用于语音识别
- 2012年:神经网络技术赢得ILSVRC(ImageNet Large Scale Visual Recognition Challenge)
深度学习的三个步骤 #
和机器学习一样:
- 确定模型(Model)/函数集(Function Set),在深度学习中就是定义一个神经网络。 不同的连接会构成多样的网络结构。
- 确定如何评价函数的好坏 如果是多分类,那和Classification一章中一样,计算每个样本预测结果与Ground Truth的交叉熵,然后求和,即为Loss。
- 确定如何找到最好的函数 还是Gradient Descent。 神经网络模型对应的函数比较复杂,而反向传播算法(Backpropagation)是一个很有效的计算神经网络梯度的方法。
神经网络的结构 #
- 输入层(Input Layer):实际上就是输入,并不是真正的“层”。
- 隐藏层(Hidden Layers):输入层和输出层之间的层,Deep指有很多隐藏层,多少层才算Deep并没有统一标准。可以看成特征提取器(Feature Extractor),作用是代替特征工程(Feature Engineering)。
- 输出层(Output Layer):最后一层,可以看成分类器
全连接前反馈神经网络 #
即Fully Connected Feedforward Neural Network,FFN。
- 全连接是指每个神经元与上一层的所有神经元相连。
- 前馈神经网络(FNN,Feedforward Neural Network)是指各神经元分层排列,每个神经元只与前一层的神经元相连,接收前一层的输出,并输出给下一层,各层间没有反馈。
一些网络 #
其中Residual Net并不是一般的全连接前馈神经网络
| 网络结构 | 提出年份 | 层数 | ImageNet错误率 |
|---|---|---|---|
| AlexNet | 2012 | 8 | 16.4% |
| 2014 | 19 | 7.3% | |
| VGGNet | 2014 | 22 | 6.7% |
| Residual Net | 2015 | 152 | 3.57% |
机器学习和深度学习面对的不同问题 #
- 在机器学习中,人类需要手工做特征工程(Feature Engineering),人类需要思考如何提取特征。
- 有了深度学习以后,人类可以不做特征工程,但也遇到了新的问题:人类需要设计合适的网络结构。
这两个问题哪个更容易呢?可能后者更容易些,比如在图像识别、语音识别任务中,人类可能并不知道自己是如何识别图像和语音的,就无法通过符号主义进行特征工程。
关于深度学习的一些疑问 #
- 虽然深度学习的的准确度很高,但是它使用的参数更多,参数多、准确度高也是很正常的事,所以有什么特别之处呢?
- 只用一个神经元足够多的隐藏层,这个模型就包括了任意函数,那为什么不这么做而非要深度呢?为什么要是Deep而不是Fat呢?
- 如何设计神经网络的结构? 多少层?每一层有多少个神经元? 只能凭经验(实验结果)和直觉,当然可以让机器自己去找网络结构,即网络架构搜索(NAS,Network Architecture Search)。
- 必须用全连接前馈神经网络吗? 不是。比如卷积神经网络(Convolutional Neural Networks, CNN)。
5.2 神经网络为什么要是深度的 #
深度的原因 #
- 矮胖的神经网络和高瘦的神经网络,假设它们参数量相同,哪一个更好呢? 2011年有一个实验,证明在参数量相当的情况下,高瘦的神经网络(即深度神经网络)的准确度更高,因为深度可以实现模块化。
- 只用一个神经元足够多的隐藏层,这个模型就包括了任意函数,那为什么不这么做呢? 这样确实可以包括任意函数,但实现的效率不高。 相关网址,也可以通过谷歌等找找其它答案。
“深度”的好处 #
模块化(Modularization) #
就像写程序一样,我们不能把所有代码写在main函数里,而需要通过定义函数等方式将程序模块化。 如下图所示,假如要做一个图片的四分类,两个维度分别是头发长短和性别,如果使用矮胖的神经网络会遇到一个问题,就是短头发的女生样本和长头发的男生样本会比较少,那这两个类别的分类器就会比较差。
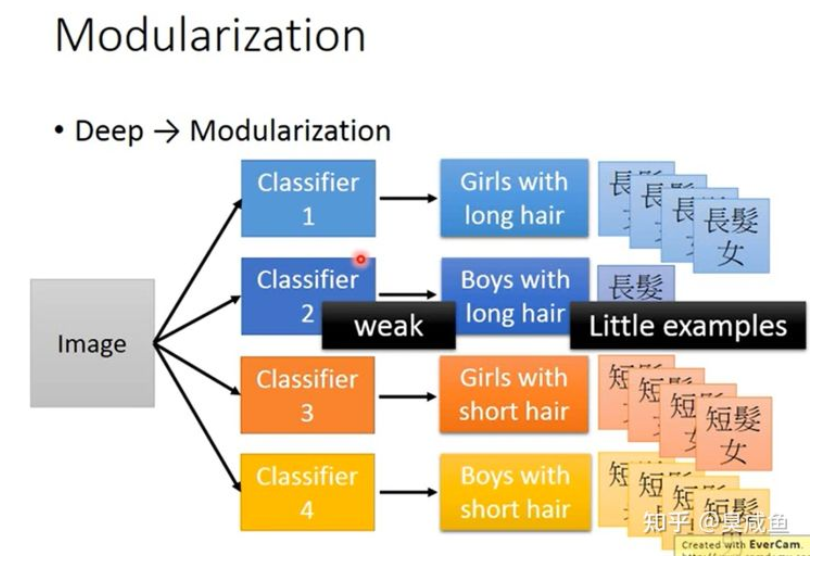
如下图所示,我们可以先定义各属性的分类器(Classifiers for the attributes),即先定义性别和头发长短的分类器,然后再做四分类。这样第一层分类器就不会遇到样本少的问题,第二层的分类器也容易训练,整体上也需要更少的训练集。
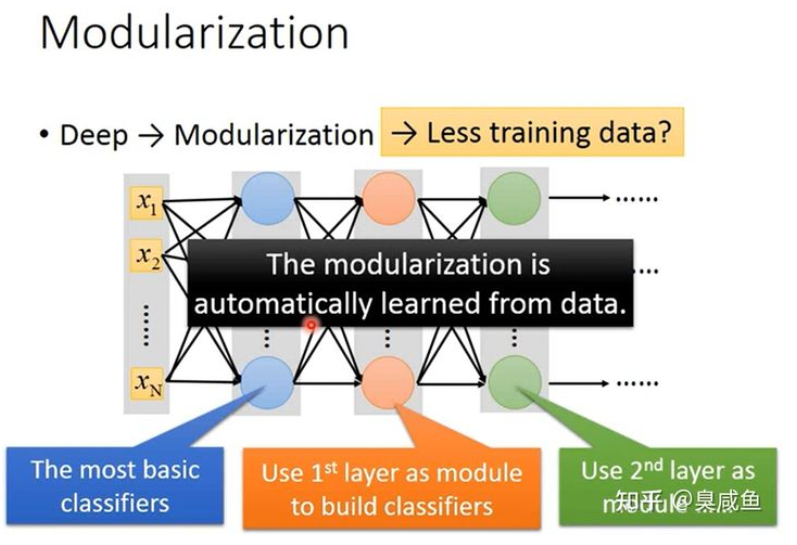
在深度神经网络中,每层网络都可以作为下一层网络使用的一个模块,并且这个模块化是通过机器学习自动得到的。 常有“人工智能=机器学习+大数据”的说法,但实际上“深度”使得需要的数据更少,如果数据集无限大,根本就不需要机器学习,只要去数据库里拿就好了。深度学习也并不是通过大量参数暴力拟合出一个模型,反而是在通过模块化有效利用数据。 这里只是一个图像分类的例子,“深度”产生的模块化在语音识别任务中也有体现,与逻辑电路也有相似的问题和结论,具体可以看** 李宏毅视频**。
端到端学习(End-to-end Learning) #
深度神经网络模型就像是把一个个函数串接在一起,每个函数负责某个功能,每个函数负责什么功能是通过机器学习根据数据自动确定的。** 李宏毅视频**中有讲这一点在语音识别、CV任务中的体现。
处理复杂任务 #
有时类似的输入要输出差别很大的结果,比如白色的狗和北极熊看起来差不多,但分类结果非常不同;有时差别很大的输入要输出相同的结果,比如火车正面和侧面的图片都应该被分类成火车。 只有一个隐藏层的网络是无法处理这种任务的。** 李宏毅视频**中有讲这一点在语音识别、CV任务中的体现。
其它 #
Do deep nets really need to be deep? ** 李宏毅视频**里也还有很多关于“深度”的探讨。
5.3 神经网络中的反向传播算法 #
链式法则(Chain Rule) #
- $\begin{cases} z=h(y)\y=g(x)\end{cases} \rightarrow \frac{dz}{dx}=\frac{dz}{dy} \frac{dy}{dx}$
- $\begin{cases} z=k(x,y)\x=g(s)\y=h(s)\end{cases} \rightarrow \frac{dz}{ds}=\frac{dz}{dx} \frac{dx}{ds}+\frac{dz}{dy} \frac{dy}{ds}$
反向传播算法(Backpropagation) #
变量定义 #
如下图所示,设神经网络输入为 $x_n$ ,该输入对应的 label 是 $\hat y^n$ ,神经网络的参数是 $\theta$ ,神经网络的输出是 $\hat y^n$ 。整个神经网络的Loss为 $L(\theta)=\sum^N_{n=1}{C^n(\theta)}$ 。假设 $\theta$ 中有一个参数 $w$ ,那 $\frac{\partial{L(\theta)}}{\partial{w}}=\sum^N_{n=1}{\frac{\partial{C^n(\theta)}}{\partial{w}}}$ 。
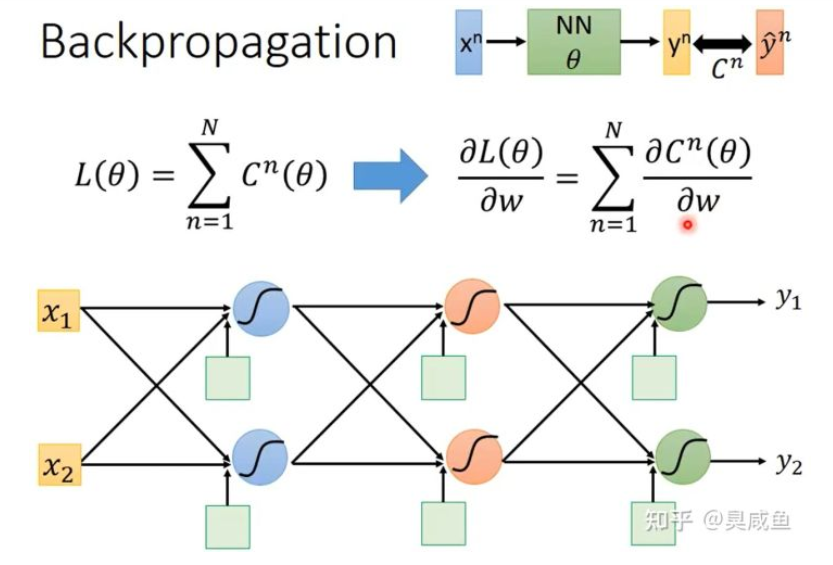
一个神经元的情况 #
如下图所示, $z=x_1w_1+x_2w_2+b$ ,根据链式法则可知 $\frac{\partial{C}}{\partial{w}}=\frac{\partial{z}}{\partial{w}}\frac{\partial{C}}{\partial{z}}$ ,其中为所有参数 $w$ 计算 $\frac{\partial{z}}{\partial{w}}$ 是 Forward Pass,为所有激活函数的输入 z 计算 $\frac{\partial{C}}{\partial{z}}$ 是 Backward Pass。
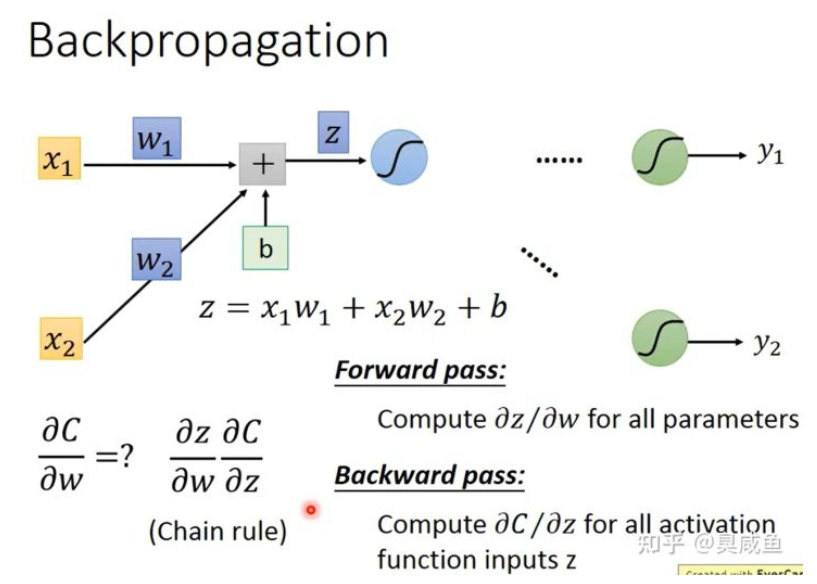
Forward Pass #
Forward Pass 是为所有参数 $w$ 计算 $\frac{\partial{z}}{\partial{w}}$ ,它的方向是从钱往后算的,所以叫做 Forward Pass。一一个神经元为例,因为 $z=x_1w_1+x_2w_2+b$ ,所以 $\frac{\partial{z}}{\partial{w_1} }= x_1 $ , $\frac{\partial{z}}{\partial{w_2} }= x_2 $ ,如下图所示。
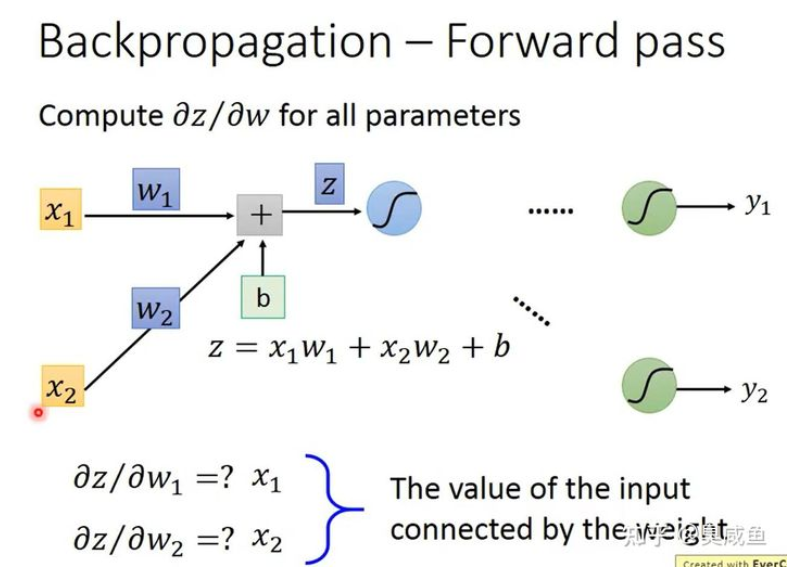
规律是:该权重乘以的那个输入的值。所以当有多个神经元时,如下图所示。
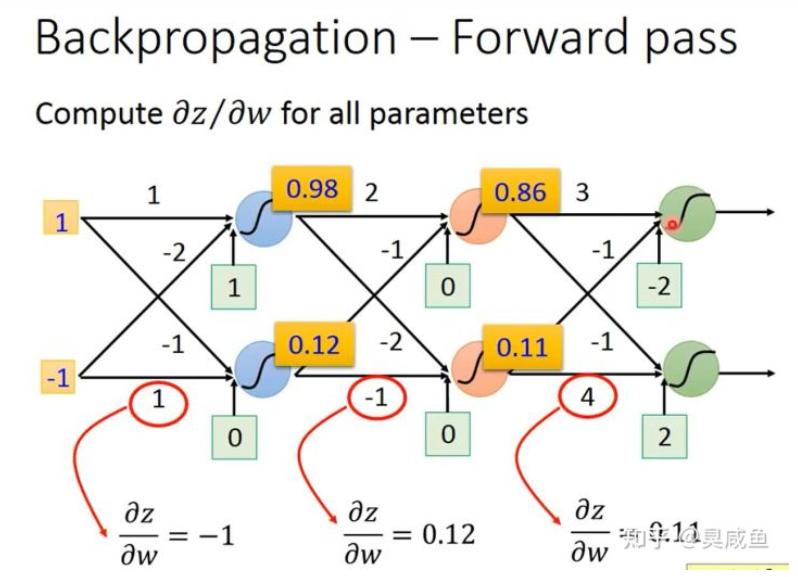
Backward Pass #
Backward Pass 是为所有激活函数的输入 z 计算 $\frac{\partial{C}}{\partial{z}}$ ,它的方向是从后往前算的,要先算出输出层的 $\frac{\partial{C}}{\partial{z’}}$ ,再往前计算它神经元的 $\frac{\partial{C}}{\partial{z}}$ ,所以叫做 Backword Pass。
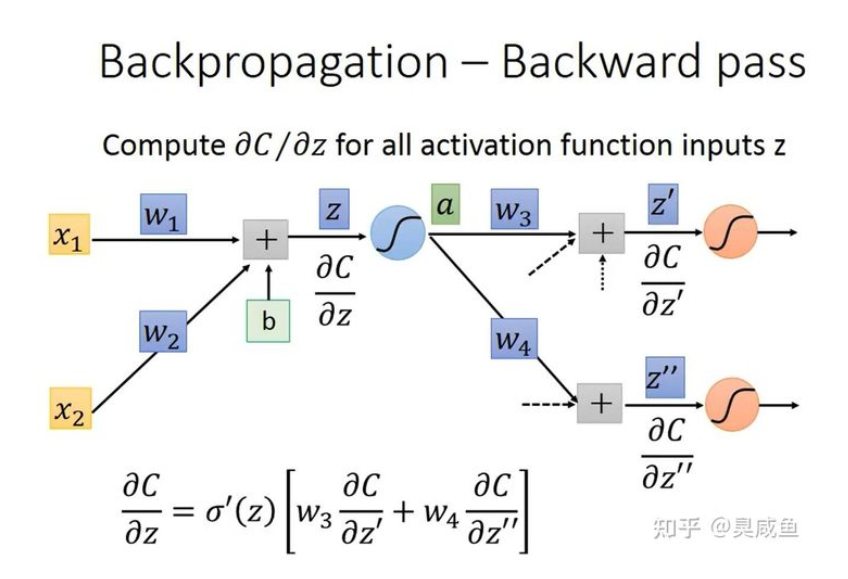
如上图所示,令 $a=\sigma(z)$ ,根据链式法则,可知 $\frac{\partial{C}}{\partial{z}}=\frac{\partial{C}}{\partial{a}}$ ,其中 $\frac{\partial{C}}{\partial{a}}=\sigma’(z)$ 是一个常数,因为在 Forward Pass 时 z 的值就已经确定了,而 $\frac{\partial{C}}{\partial{a}}=\frac{\partial{z}’}{\partial{a}}\frac{\partial{C}}{\partial{z}’}+\frac{\partial{z}’’}{\partial{a}}\frac{\partial{C}}{\partial{z}’’}=w_3\frac{\partial{C}}{\partial{z}’}+w_4\frac{\partial{C}}{\partial{z}’’}$ ,所以 $ \frac{\partial{C}}{\partial{z}}=\sigma’(z)[w_3\frac{\partial{C}}{\partial{z}’}+w_4\frac{\partial{C}}{\partial{z}’’}]$ 。
对于式子 $\frac{\partial{C}}{\partial{z}}=\sigma’(z)[w_3\frac{\partial{C}}{\partial{z}’}+w_4\frac{\partial{C}}{\partial{z}’’}]$ ,我们可以发现两点:
1、$\frac{\partial{C}}{\partial{z}}$ 的计算式是递归的,因为在计算 $\frac{\partial{C}}{\partial{z}}$ 的时候需要计算 $\frac{\partial{C}}{\partial{z}’}$ 和 $\frac{\partial{C}}{\partial{z}’’}$ 。如下图所示,输出层的 $\frac{\partial{C}}{\partial{z}’}$ 和 $\frac{\partial{C}}{\partial{z}’’}$ 是容易计算的。
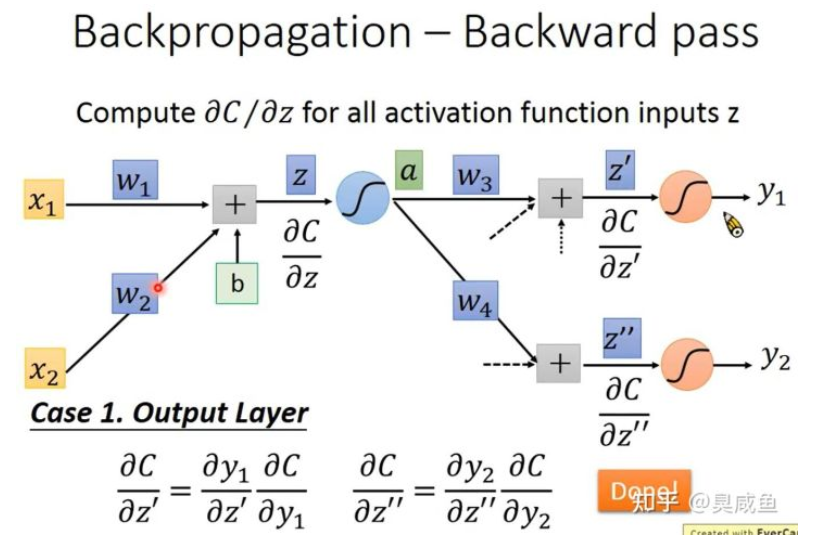
2、$\frac{\partial{C}}{\partial{z}}$ 的计算式 $\frac{\partial{C}}{\partial{z}}=\sigma’(z)[w_3\frac{\partial{C}}{\partial{z}’}+w_4\frac{\partial{C}}{\partial{z}’’}]$ 是一个神经元的形式。如下图所示,只不过没有嵌套 sigmoid 函数,而是乘一个常数 $\sigma’(z)$ ,每一个 $\frac{\partial{C}}{\partial{z}}$ 都是一个神经元的形式,所以可以通过神经网络计算 $\frac{\partial{C}}{\partial{z}}$ 。

总结 #
- 通过Forward Pass ,为所有参数 $w$ 计算 $\frac{\partial{z}}{\partial{w}}$ ;
- 通过 Backward Pass ,为所有激活函数的输入 z 计算 $\frac{\partial{C}}{\partial{z}}$ ;
- 最后通过 $\frac{\partial{C}}{\partial{w}}=\frac{\partial{z}}{\partial{w}}\frac{\partial{C}}{\partial{z}}$ ,也就求出了梯度。
