2.1 线性回归模型 #
回归模型应用案例 #
- 股票市场预测(Stock Market Forecast):预测某个公司明天的股票情况
- 自动驾驶车(Self-Driving Car):预测方向盘的转动角度
- 推荐系统(Recommendation):预测某用户购买某商品的可能性
线性回归模型(Linear Regression Model) #
形式如下: $y= f(x) = w \cdot x + b $
- y是输出,$\widehat{y}$ 是真实值/标签(label)
- w是权重(weight)
- b是偏置(bias)
- x是输入(input),也可叫做特征(feature)。数据集中一般包含多个object,每个object一般包含多个component。此时,上标是object的索引,下标是component的索引
- 损失函数(Loss Function)如果不考虑模型的好坏,衡量一个函数的好坏,其实是衡量模型参数的好坏。以线性模型为例,就是衡量参数和的好坏。如 $ L(f) = L(w,b) = \sum_{n=1} ^{10}{ \widehat{y} - (b + w \cdot x_n)} $ ,把所有的样本误差的平方和作为损失函数
- 输入:一个函数
- 输出:多么地不好(how bad it is)。损失函数值越大,则这个函数越差、与数据集中内容月不相符
梯度下降(Gradient Descent) #
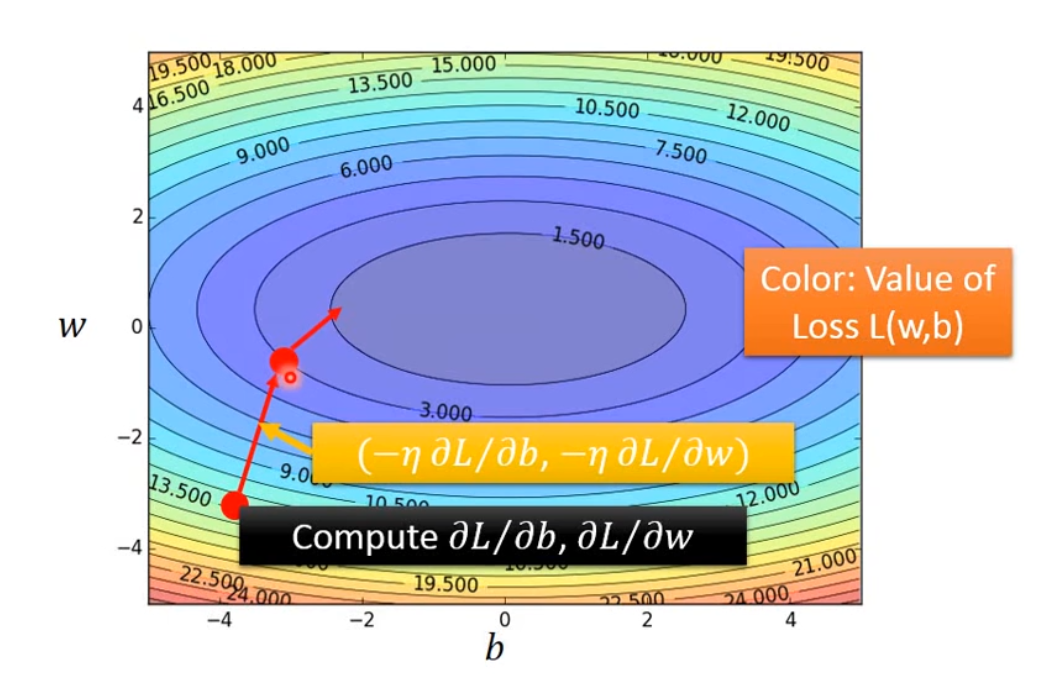
梯度下降可以优化损失函数的值,使其尽量小,即可找到最好(在数据集上模拟效果最好)的模型参数。 现在假设模型$f$中只有一个参数 $w$,则损失函数为$L(f) = L(w)$ ,梯度下降算法如下
- 初始化参数:随机选取一个 $ w_0 $(并不一定是随机选取),令 $ w = w_0 $
- 计算梯度 $\frac{dL(f)}{dw}|_{w=w_0}$ ,如果小于0,此时w增大则L(f)减小,如果大于0,此时w减小则L(w)会减小。如果模型中有多个参数,则计算损失函数在各个参数方向上的偏导数
- 更新模型参数,$w_1 = w_0 - lr \frac{dL(f)}{dw}|_{w=w_0}$ ,w的变化量取决于梯度和学习率(Learning Rate)的大小:梯度绝对值或学习率越大,则w变化量越大。如果模型有多个参数,则用上一步计算出的偏导数对应更新各参数。
- 重复第2步和第3步,经过多次参数更新/迭代(iteration),可以使损失函数的值达到局部最小(即局部最优,Local Optimal),但不一定是全局最优。
现在假设模型$f$中只有两个参数 $w$,则损失函数为$L(f) = L(w)$ ,梯度下降算法如下(若模型中有多个参数,按相同方法更新各参数)
- 初始化参数:随机选取初始值$w_0$和$b_0$(并不一定是随机选取),令$w = w_0$,$b=b_0$
- 计算梯度 $ \frac{dL(f)}{dw}|{w=w_0,b=b_0} $, $ \frac{dL(f)}{db}|{w=w_0,b=b_0} $
- 更新模型参数,$ w_1 = w_0 - lr \frac{dL(f)}{dw}|{w=w_0,b=b_0} $ , $ b_1 = b_0 - lr \frac{dL(f)}{db}|{w=w_0,b=b_0} $ 。
- 重复第2步和第3步,经过多次参数更新/迭代(iteration),可以使损失函数的值达到局部最小(即局部最优,Local Optimal),但不一定是全局最优。
2.2 如何选择模型、减小误差 #
模型选择(How to select model) #
- 模型越复杂,一般在训练集上的误差(Error)越小。因为更复杂的模型(函数集)包含更多的函数。比如二次模型包含一次模型
- 模型越复杂,其在测试集上的误差(Error)不一定越小,因为模型过于复杂时,越容易被数据影响,可能导致过拟合。
误差(Error) #
误差的来源 #
暂时称通过机器学习得到的函数为人工函数,它其实是对“上帝函数”的估计(Estimator),和“上帝函数”之间是有误差的。
误差来源于两方面:一是Bias,二是Variance,需要权衡(trade-off)两者以使总误差最小。
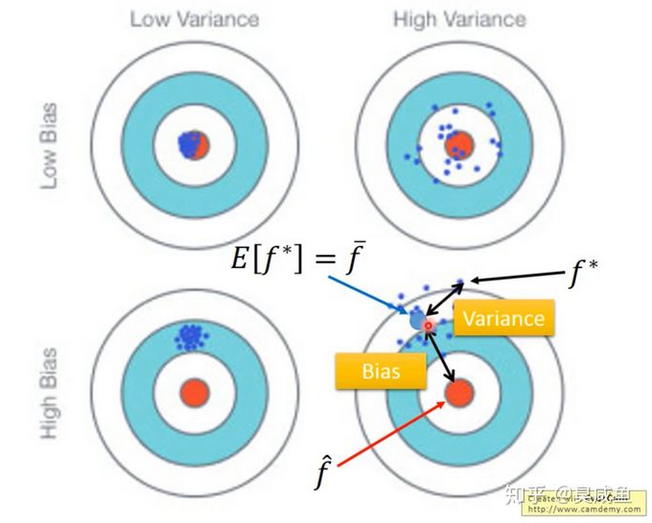
如上图所示,Bias是指人工函数(的期望)和上帝函数之间的距离,Variance是指人工函数的离散程度(或者说是不稳定程度)
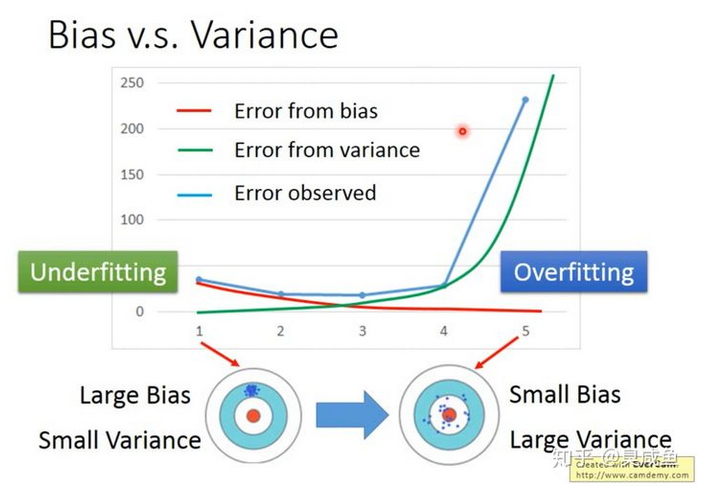
如上图所示,横轴是模型的复杂程度(1次幂、2次幂、……),纵轴是误差大小。模型越复杂,Bias越小,Variance越大。
Variance #
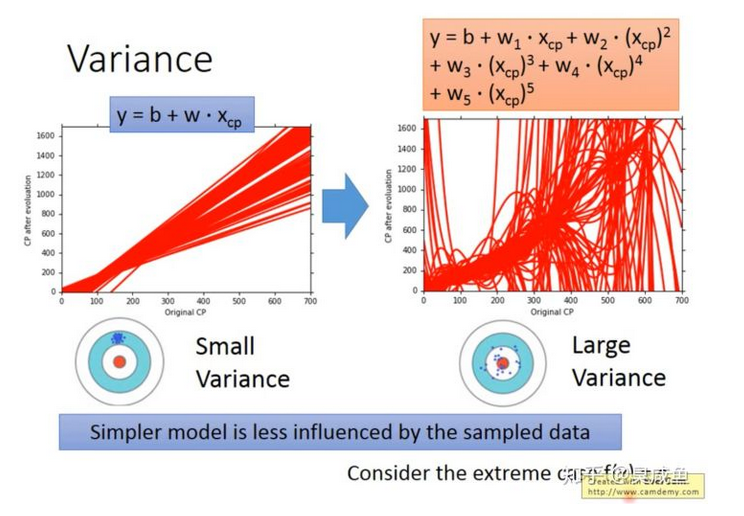
使用相同模型在不同数据上拟合得到的函数是不同的,这些函数之间的离散程度就是Variance。以射箭为例,Variance衡量的就是射得稳不稳。模型越复杂,Variance越大。因为模型越简单,越不容易被数据影响(对数据不敏感,感知数据变化的能力较差),那Variance就越小。
Bias #
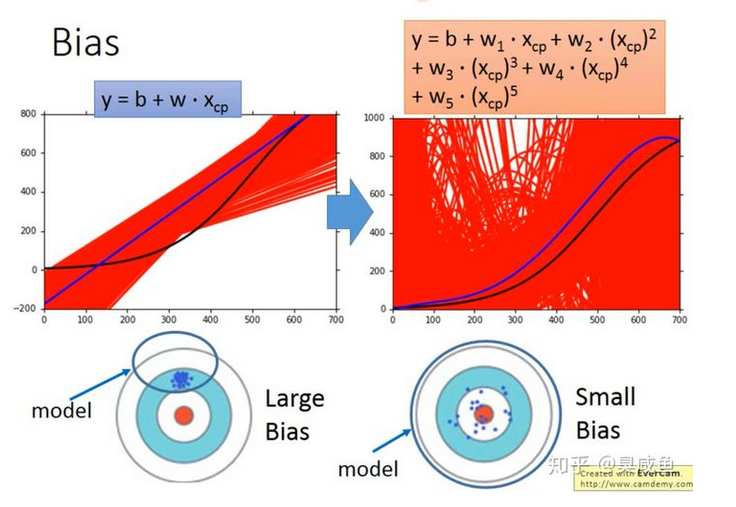
使用相同模型在不同数据上拟合得到的函数是不同的,取这些函数的“期望”,该期望与“真理”的差距就是Bias。以射箭为例,Bias衡量的就是射得准不准(这里的“准”的含义有待商榷)。**模型越简单,Bias越大。**因为模型就是个函数集(Function Set)。模型越简单,则其包含的函数就越少、包含“上帝函数”的几率就越小,甚至可能不包括上帝函数。
在函数集很小的情况下,即使是其中最好的函数,它与“上帝函数”的差距也还是很大的。
2.3 欠拟合与过拟合 #
欠拟合(Underfitting) #
Bias较大、Variance较小。如果模型在训练集上的误差很大,则此时Bias是大的,情况为欠拟合。
Bias大时如何处理:使用更复杂的模型,比如添加考虑更多维度的输入、把线性模型换成非线性模型。
过拟合(Overfitting) #
Bias较小、Variance较大。如果模型在训练集上的误差很小,但是在测试集上的误差很大,则此时Variance是大的,情况为过拟合。
Variance大时如何处理:
- 使用更复杂的数据集:比如添加数据(很有效,但不一定做得到)、数据增强等方法。
- 使用更简单的模型(不是根本方法),可能是模型过于复杂导致了过拟合,因此可以简化模型缓解过拟合。
- 正则化(Regularization):正则化可能会使Bias增大,所以需要调整正则化的参数。如$L_{new} = L_{old} + \lambda \sum{w_i^2}$ ,其中$\lambda$ 是一个常数。加上正则项 $\lambda \sum{w_i^2}$ 的目的是让函数参数尽可能地接近0,使函数变得平滑。
平滑(Smooth) #
平滑是指输入变化影响输出变化的程度(输出对输入的敏感程度)。假设输入变化,如果函数越不平滑,则输出变化程度越大。函数参数越接近0,这个函数就越平滑(smooth)。
- 我们为什么喜欢一个平滑的函数?适度平滑的函数可以缓解函数输入中包含的噪声对函数输出的影响。如果输入中包含一些噪声/干扰(noise),那平滑函数的输出受输入中包含的噪声干扰的程度更小。
- 我们为什么不喜欢过于平滑的函数?函数过于平滑,就无法有效地提取数据的特征,这不是我们想要的函数。假设有一个极限平滑的函数,即该函数的输出不受输入的影响,那当然不是个好的函数。
2.4交叉验证 #
在机器学习中,同城不能将全部数据用于模型训练,否则将没有数据集可以用来评估模型
The Validation Set Approach #
将数据集划分成训练集(Training Set)和测试集(Test Set)两部分。
缺点:这种方法的缺点是依赖于训练集和测试集的划分方法,并且只用了部分数据进行模型的训练。
LOOCV(Leave One Out Cross Validation) #
假设数据集中有N个数据,取其中1个数据作为测试集,将剩下的N-1个数据作为训练集,这样重复N次就得到N个模型以及N个误差值,最终使用这N个误差值的平均值评估该模型。
优点:该方法不受训练集和测试集划分方法的影响,因为每个数据都单独做过测试集;同时该方法用了N-1个数据训练模型,也几乎用到了所有的数据,保证了模型的Bias更小。
缺点:该方法的缺点是计算量过大,是The Validation Set Approach耗时的N-1倍。
K折交叉验证(K-fold Cross Validation) #
该方法是LOOCV的折中,即将数据集分成K份。
如何选取K的值:K的选取是一个Bias和Variance的trade-off。一般选择K=5或10。K越大,每次训练时训练集的数据量就越大,则Bias越小;但每次训练时的训练集之间的相关性越大(考虑最极端的情况K=N,也就是LOOCV,每次训练使用的数据几乎是一样的),这种大相关性会导致最终的误差具有更大的Variance。
