Beta分布是一个概率的概率分布,其范围限制在0和1之间。例如,我们可以使用它来建模概率:
- 广告的点击率;
- 网站上购买的客户的转化率;
- 读者为您的博客点赞的可能性;
- 特朗普赢得一次竞选的可能性;
- 乳腺癌女性的5年生存机会;
- 依此类推。

让我们暂时忽略系数 $\frac{1}{Beta(\alpha, \beta)}$ ,只看分子 $x^{\alpha - 1}(1-x)^{\beta - 1}$,因为 $\frac{1}{Bata(\alpha, \beta)}$ 只是使该函数积分为 $1$ 的规格化常数。然后,分子中的术语 $-x$ 表示某的幂乘以 $1-x$ 表示某的幂看起来很熟悉。
当我们从二项式分布的角度来看时,Beta分布的直觉就起作用了。

二项式和Beta之间的区别在于,前者对成功次数(x)进行建模,而后者对成功概率(p)进行建模。 换句话说,概率是二项式的参数;在Beta中,概率是一个随机变量。
解释 $\alpha$、$\beta$
你能想到的 $\alpha-1$ 作为成功的数目和 $\beta-1$ 作为失败的次数,就像ñ&NX二项式条款。 您可以选择 $\alpha$ 和 $\beta$ 参数,但是您认为它们应该是。如果你觉得成功的概率是非常高的,比方说 $90%$,设置 $90 \alpha$ 和 $10 \beta$。否则,$\beta$ 为90,$\alpha$ 为10。 随着 $\alpha$ 变大(成功事件越多),概率分布的大部分将向右移动,而β的增加则使分布向左移动(更多的失败)。 同样,如果我们同时确定 $\alpha$ 和 $\beta$ 都增加,则分布将变窄。
2. 例子:概率的概率
假设某人同意与您约会的可能性是,$\beta$ 分布为 $\alpha = 2$,$\beta = 8$。您的成功率大于 $50%$ 的概率是多少?
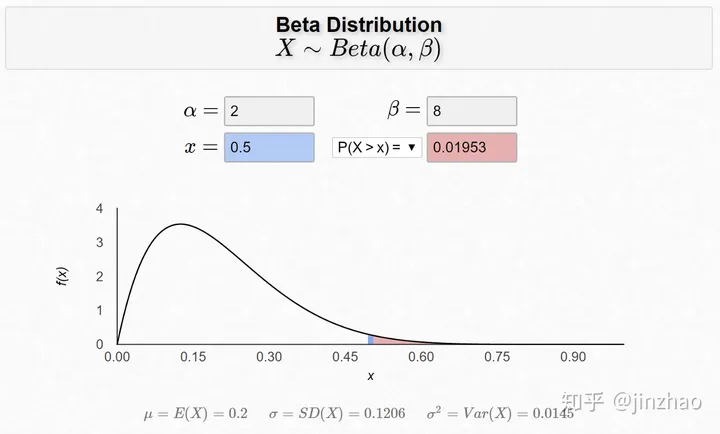
$P(X > 0.5)= 1- CDF(0.5)= 0.01953$ 对不起,这很低。
爱荷华大学的Bognar博士为Beta分布构建了demo,我发现它实用且美观。您可以试验不同的α和β值,并可视化形状变化。
3. 为什么我们使用Beta分布?
如果我们只希望概率分布对概率建模,那么 $(0,1)$ 上的任何任意分布都将起作用。创建一个应该很容易。只需取任何不会在 $0$ 到 $1$ 之间爆炸并保持正值的函数,然后将其从 $0$ 积分到 $1$ ,然后简单地将该函数除以该结果即可。您刚刚获得了可用于对概率进行建模的概率分布。在那种情况下,为什么我们坚持在任意概率分布上使用beta分布?
Beta分布有何特别之处?
Beta分布是贝叶斯推断中伯努利,二项式,负二项式和几何分布(似乎是涉及成功与失败的分布)的共轭先验。
使用共轭先验计算后验非常方便,因为您可以避免贝叶斯推理中涉及的太多的数值计算。
共轭先验
讨论概率分布的一个重要原因是,现实生活中有很多数据可以使用这些模型来模拟。对于给定的一个数据集合 $x_1,…,x_n$ 我们希望这个数据集合来自于某个随机变量 $X$ ,并且这个随机变量具有概率分布 $P(X)$。找到 $P(X)$ 的过程叫做密度估计(density estimation)。需要强调的是密度估计问题是一个病态问题,因为世界上的概率密度函数不计其数,能够给出观测集合 $x_1,…,x_n$ 的概率密度函数也是如此之多。任何一个在 $x_1,…,x_n$ 处非零的密度函数 $P(X)$ 都可能是候选。选择一个合适的 $P(X)$ 是模型选择问题,在机器学习领域经常遇见。
