瑞士数学家雅克·伯努利(Jacques Bernoulli, 1654~1705)首次研究独立重复试验(每次成功率为$p$ )。在他去世后的第 $8$ 年(1713年),他侄子尼克拉斯出版了伯努利的著作《推测术》。在书中,伯努利指出了如果这样的试验次数足够大,那么成功次数所占的比例以概率 $1$ 接近 $p$。 雅克·伯努利是这个最著名的数学家庭的第一代。在后来的三代里,一共有 $8$ 到 $12$ 个伯努利,在概率论、统计学和数学上做出了杰出的基础性贡献。
伯努利分布在一次试验中,事件 $A$ 出现的概率为 $p$,不出现的概率为 $q=1-p$。若以 $\beta$ 记事件 $A$ 出现的次数,则 $\beta$ 仅取 $0, 1$ 两值,相应的概率分布为:
$$ P(\beta = k) = \begin{cases} p & \text{if } k = 1 \ 1-p & \text{if } k = 0 \end{cases} $$
其中 $k \in {0, 1}$。
二项分布是指在只有两个结果的 $n$ 次独立的伯努利试验中,所期望的结果出现次数的概率。在单次试验中,结果A出现的概率为 $p$ ,结果B出现的概率为 $q$,$p+q=1$。那么在 $n=10$ ,即 $10$ 次试验中,结果A出现 $0$ 次、$1$ 次、……、$10$ 次的概率各是多少呢?这样的概率分布呈现出什么特征呢?这就是二项分布所研究的内容。
还是先举个例子吧。
掷一枚硬币(怎么老是硬币?小学的时候就讲了)出现正面和反面的概率各为 $0.5$ ,那么掷 $1$ 次,出现正面的概率肯定是 $0.5$ 。掷 $2$ 次、掷 $3$ 次呢?
掷 $2$ 次出现的结果有 $4$ 个,正正、正反、反正、反反。因为 $p=0.5$,所以每个结果出现的概率是 $0.5×0.5=0.25$,那正面出现 $2$ 次、$1$ 次、$0$ 次的概率分别是 $0.25$ 、$0.5$ 、$0.25$ 。
掷3次出现的结果有8个,正正正、正正反、正反正、正反反、反正正、反正反、反反正、反反反。每个结果出现的概率是 $0.5×0.5×0.5=0.125$ ,那正面出现 $3$ 次、$2$ 次、$1$ 次、$0$ 次的概率分别是 $0.125$、$0.375$、$0.375$、$0.125$。
统计学家们总结出了计算概率的一般公式
$$ b(x,n,p) = C_n^x p^x q^{n-x} $$
其中 $b$ 表示二项分布的概率,$n$ 表示试验次数,$x$ 表示出现某个结果的次数。是组合,表示在 $n$ 次试验中出现 $x$ 次结果的可能的次数。如 $10$ 次试验,出现 $0$ 次正面的次数有 $1$ 次,出现 $1$ 次正面的次数有 $10$ 次,……,出现 $5$ 次正面的次数有 $252$ 次,等等。其计算也有一个通式:
$$ C_n^x=\frac{n \times (n-1) \times … \times (n-x-1)}{x \times (x-1) \times … \times 1} $$
也可以写成
$$ C_n^x=\frac{n!}{(n-x)!x!} $$
如果这个公式你算不好,就查下面的杨辉三角形吧,每一行的数字是上一行相邻两个数字的和。在下图中,每一行表达的是 $(a+b)^n$ 展开式的各项系数,下图列出了 $n=0,1,…,16$ 时展开式中各项的系数。

需要特别提醒的是:二项分布是建立在有放回抽样的基础上的,也就是抽出一个样品测量或处理完后再放回去,然后抽下一个。在实际的工作中通常我们很少会这样抽,一般都属于无放回抽样,这时候需要用超几何分布来计算概率。在一般的教课书上都会要求,
- 当总体的容量 $N$ 不大时,要用超几何分布来计算,
- 如果 $N$ 很大而 $n$ 很小,则可以用二项分布来近似计算,也就是可以将无放回抽样近似看出有放回抽样。至于 $n$ 要小到什么程度,有的书上说 $n/N$ 小于 $0.1$ 就可以了,有的书上则要求小于 $0.05$。
在很多工厂里,通常都会跟零件供应商约定供货合格率,并对每批供货进行抽检,就是所谓的 $IQC$ 。设约定的合格品率为 $97%$ ,如果每批随机抽 $10$ 件,那么抽出 $1$ 件不合格时,整批的零件的合格率是不是达不到 $97%$?
根据题意,$p=0.97$,$n=10$,$x=9$,据此算出 $10$ 个样品中有 $9$ 个合格品的概率是
$$ b(9,10,0.97) = C_{10}^9 \times 0.97^9 \times 0.03^1 = 0.228 $$
反过来,如果考虑不合格品率,$p=0.03$,$n=10$,$x=1$,据此计算出 $10$ 个样品中有 $1$ 个不合格品的概率是
$$ b(1,10,0.03) = C_{10}^1 \times 0.03^1 \times 0.97^9 = 0.228 $$
结果是一样的。由此可见,$10$ 个样品中有 $1$ 个不合格品的概率还是很大的,因此不能说这批零件不合格。
那抽出 $2$ 个不合格的呢?同样可以算出
$$ b(2,10,0.03) = C_{10}^2 \times 0.03^2 \times 0.97^8 = 0.032 $$
概率非常小,而且抽出超过 $2$ 个以上不合格品的概率会更小,因此如果 $10$ 个样品中有 $2$ 个或以上的不合格品,则整批的零件合格率肯定达不到 $97%$ ,可以整批退货。
如果约定的合格率是 $99.5%$ ,则出现 $0$ 个、$1$ 个、$2$ 个不合格品的概率分别为 $0.951$ 、$0.0478$ 、$0.001$,如此 $10$ 个只要抽出 $1$ 个不合格品就可以整批退货了。
有人会问,到底应该抽多少样呢?这在GB/T2828里有明确规定,限于篇幅,这里只介绍其中一种最简单的应用原理,具体应用时大家可以去查国标。
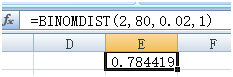
- 假设你与供应商约定的接收合格率是 $99%$ ,即 $AQL(接收质量限)=0.01$ ,本批的总数量是 $1000$ 只,只做一般性的检验,查国标可得抽样量为 $80$ ;
- $Ac=2$,即抽到2个及以下不合格品可接收该批;
- $Re=3$,即抽到3个及以上不合格品则拒绝接收。
限于人力物力,你可能无法抽这么多的样,根据该供应商以往的表现,你制定了两种抽样方案,
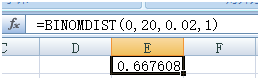
- 一种是抽 $20$ 个,不合格品为 $0$ 接收,大于 $0$ 退回;
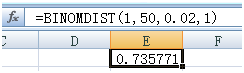
- 另一种是抽 $50$ 个,不合格品不超过 $1$ 则接收,大于 $1$ 则退回。
我们来看看,如果这批来料合格率只有 $98%$ ,按照这两种抽样方案以及国标的方案,你接收的概率有多大。为了方便我们用Excel来算。
方案一
方案二
国标方案
这几种方案接收的概率都不小,这就是抽样检验带来的风险。如果实际批合格率低于约定合格率,仍被接收的风险属于使用者风险。
反过来,如果批合格率高于约定合格率,如99.5%,那有多大的可能性拒绝该批呢?我们也可以用二项分布来计算。

我们可以看到,即使实际合格率高于约定,仍然存在拒收的风险,虽然这个风险并不大,通常这一类的风险叫做生产者风险。
根据不同的批合格率,可以计算出每一种抽样方案的两类风险,画出OC曲线。用方案一画出的OC曲线如下:
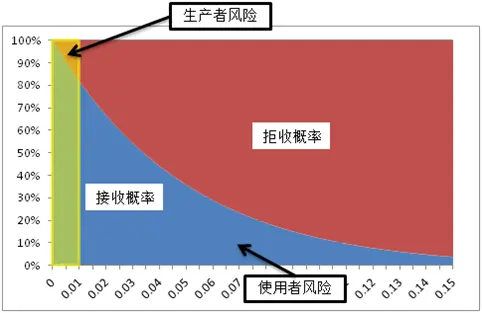
图中横坐标为实际的批不合格率,纵坐标为接收概率,曲线下方为接收概率,上方为拒收概率,可以看出即使来料不合格率远高于约定,接收的概率还是很大的。黄色的矩形框称为理想曲线,理想的情况下,批不合格率低于约定肯定接收,而超过约定则肯定拒收,但这种理想曲线是不可能达到的,只能尽可能接近。
下面我们再看看三种抽样方案的OC曲线之间的对比。
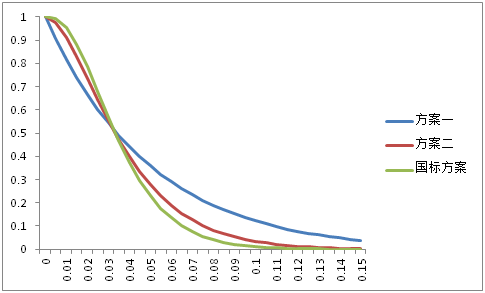
三种方案各有优劣势,但国标方案的下降趋势要比另外两种要快,更接近理想曲线。当然你也可以试一下其它的抽样方案,有可能会找到更好的。
确定抽样方案不是靠拍脑袋来决定的,需要对抽样方案进行比较深入的研究,找到最恰当的抽样方案。
另外,关于抽样问题要具体问题具体分析,如果供应商质量控制能力很强,可以放宽检验甚至免检(可以将此作为供应商的激励措施,这也是我在客户那里极力推动的,虽然这项政策最终是依据国内一个质量大腕的建议制定的,我仍然觉得非常高兴);如果供应商质量控制能力很差,就需要加严检验。有时要控制误检,有时要控制漏检,这要看成本与收益。我曾经服务的一家客户对一个零件专门配10个人进行全检,就是为了防止漏检,因为必须要100%合格,否则因为漏检造成客户的索赔是承受不起的。
本文所描述的仅仅是国标中最基本、最简单的应用,当遇到各种复杂的情况时,要想到去参考国标。
最后再说一下二项分布的正态近似。在大样本的情况下,二项分布的计算会很麻烦,这时可以采用正态分别来近似,其条件是np和n(1-p)都大于5。采用正态分布的参数为:
$$ \mu=np, \sigma=\sqrt{np(1-p)} $$
