- 题目链接:https://www.nowcoder.com/exam/company?currentTab=recommand&jobId=100&selectStatus=0&tagIds=179
这次的笔试,很多签到题,没什么难度,主要是第 3 题和第 9 题,比较有难度。
3.小美的树上染色 #

在做的时候,很幸运的从后往前遍历就过了,应该是用例水了。
import java.util.Scanner;
import java.util.*;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNextInt()) {
int n = in.nextInt();
int[] a = new int[n];
int u, v;
Set<Integer> temp = new HashSet<>();
for (int i = 0; i < n; i++) {
a[i] = in.nextInt();
}
int ans = 0;
int [][]conn = new int[n - 1][2];
for (int i = 0; i < n - 1; i++) {
conn[i][0] = in.nextInt();
conn[i][1] = in.nextInt();
conn[i][0] -= 1;
conn[i][1] -= 1;
}
for (int i = n-2; i >= 0; i--) {
if ( !temp.contains(conn[i][0]) && !temp.contains(conn[i][1])
&& Math.pow((int)Math.sqrt(a[conn[i][0]] * a[conn[i][1]]),
2) == (a[conn[i][0]] * a[conn[i][1]]) ) {
temp.add(conn[i][0]);
temp.add(conn[i][1]);
ans+=2;
}
}
System.out.println(ans);
}
}
}
1. 树形DP解法 #
树形DP的好题。
对于每个节点,引入0,1状态(表示不染色,染色)
那每个子树的根节点u, s为u的儿子节点集合

import java.io.BufferedInputStream;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
public class Main {
static class Solution {
int[] ws;
List<Integer> []g;
int[][] dp;
int solve(int n, int[] ws, List<Integer>[] g) {
this.g = g;
this.dp = new int[n + 1][2];
this.ws = ws;
dfs(1, -1);
return Math.max(dp[1][0], dp[1][1]);
}
void dfs(int u, int fa) {
int[] res = new int[] {0, 0};
for (int v: g[u]) {
if (v == fa) {
continue;
}
dfs(v, u);
res[0] += Math.max(dp[v][0], dp[v][1]);
}
for (int v: g[u]) {
if (v == fa) continue;
int x2 = res[0] - Math.max(dp[v][0], dp[v][1]);
long rr = (long)ws[u] *ws[v];
long r = (long)Math.sqrt(rr);
if (r * r == rr) {
res[1] = Math.max(2 + x2 + dp[v][0], res[1]);
}
}
dp[u][0] = res[0];
dp[u][1] = res[1];
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int n = sc.nextInt();
int[] ws = new int[n + 1];
for (int i = 1; i <= n ;i++) {
ws[i] = sc.nextInt();
}
List<Integer>[]g = new List[n + 1];
Arrays.setAll(g, x -> new ArrayList<>());
for (int i = 0; i < n - 1; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
g[u].add(v);
g[v].add(u);
}
Solution solution = new Solution();
int res = solution.solve(n, ws, g);
System.out.println(res);
}
}
2. 无权二分图最大匹配 #
看到评论区有大佬,提到了这个方法,所以补充一下。
匈牙利算法,其时间复杂度 $O(V*E)$, 树的节点$N$,边$N-1$,理论会达到$O(10^{10})$。
感觉还是测试数据偏随机,完全平方数限制很强,导致时间复杂度骤降。
import java.io.BufferedInputStream;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
public class Main {
// 无权二分图最大匹配算法 O(VE)
static boolean match(int u, int[] link, boolean[] used, List<Integer> []g) {
for (int v: g[u]) {
if (used[v]) continue;
used[v] = true;
if (link[v] == 0 || match(link[v], link, used, g)) {
link[u] = v;
link[v] = u;
return true;
}
}
return false;
}
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int n = sc.nextInt();
int[] ws = new int[n + 1];
for (int i = 1; i <= n ;i++) {
ws[i] = sc.nextInt();
}
List<Integer>[]g = new List[n + 1];
Arrays.setAll(g, x -> new ArrayList<>());
for (int i = 0; i < n - 1; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
long rr = (long)ws[u] * ws[v];
long r = (long)Math.sqrt(rr);
if (r * r == rr) {
g[u].add(v);
g[v].add(u);
}
}
int ans = 0;
int[] link = new int[n + 1];
for (int i = 1; i <= n; i++) {
if (link[i] != 0) continue;
boolean[] used = new boolean[n + 1];
used[i] = true;
if (match(i, link, used, g)) {
// 找到一条增广路径
ans++;
}
}
System.out.println(ans * 2);
}
}
9.小美的字符串变换 #
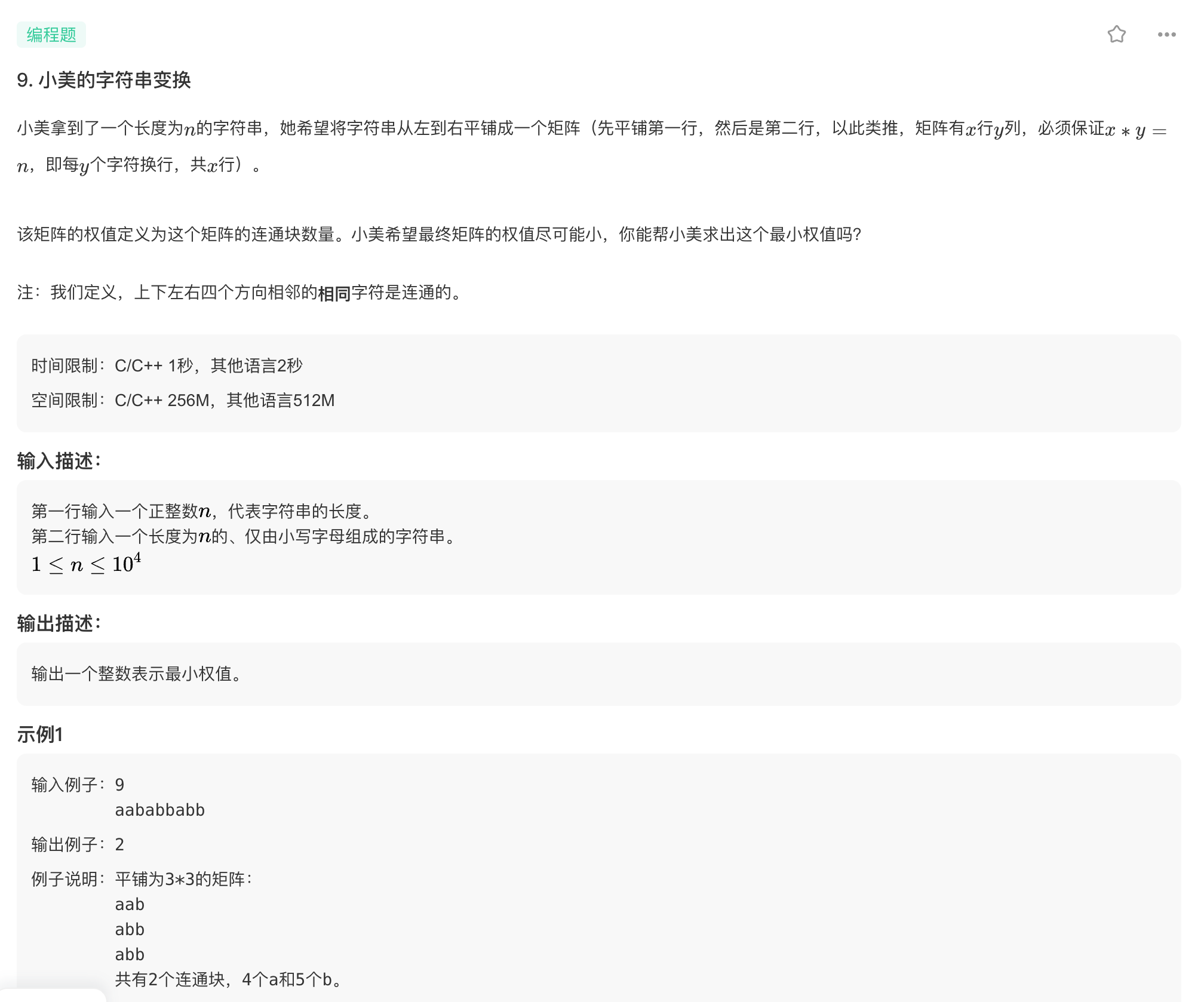
此题是经典的并查集模板题。首先生成行列乘积为n的二阶矩阵,再根据矩阵中元素上下左右值是否与之相等选择是否union,最后得到并查集中集合数量。取所有二阶矩阵并查集中集合数量最小值即为解。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
char[] str = sc.next().toCharArray();
int q = n;
for (int i = 1; i <= n; i++) {
if (n % i == 0) {
int N = i;
int M = n / i;
int[][] board = new int[N][M];
int index = 0;
for (int j = 0; j < N; j++) {
for (int k = 0; k < M; k++) {
board[j][k] = str[index++];
}
}
q = Math.min(q, q(board));
}
}
System.out.println(q);
}
public static int q(int[][] board) {
int N = board.length;
int M = board[0].length;
UnionFind uf = new UnionFind(N * M);
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
int cur = i * M + j;
if (i - 1 >= 0 && board[i - 1][j] == board[i][j]) {
uf.union(cur - M, cur);
}
if (i + 1 < N && board[i + 1][j] == board[i][j]) {
uf.union(cur + M, cur);
}
if (j - 1 >= 0 && board[i][j - 1] == board[i][j]) {
uf.union(cur - 1, cur);
}
if (j + 1 < M && board[i][j + 1] == board[i][j]) {
uf.union(cur + 1, cur);
}
}
}
return uf.size();
}
public static class UnionFind {
private int[] parent;
private int[] sizeMap;
private int size;
public UnionFind(int N) {
size = N;
parent = new int[N];
sizeMap = new int[N];
for (int i = 0; i < N; i++) {
parent[i] = i;
sizeMap[i] = 1;
}
}
public int size() {
return size;
}
private int find(int v) {
if (v != parent[v]) {
parent[v] = find(parent[v]);
}
return parent[v];
}
public void union(int v1, int v2) {
int f1 = find(v1);
int f2 = find(v2);
if (f1 != f2) {
size--;
int s1 = sizeMap[f1];
int s2 = sizeMap[f2];
if (s1 > s2) {
parent[f2] = f1;
sizeMap[f1] += s2;
} else {
parent[f1] = f2;
sizeMap[f2] += s1;
}
}
}
}
}
